Τύπος παραλλαγής χαρτοφυλακίου (παράδειγμα) | Πώς να υπολογίσετε τη διακύμανση χαρτοφυλακίου;
Τι είναι η διακύμανση χαρτοφυλακίου;
Ο όρος «διακύμανση χαρτοφυλακίου» αναφέρεται σε μια στατιστική αξία της σύγχρονης επενδυτικής θεωρίας που βοηθά στη μέτρηση της διασποράς των μέσων αποδόσεων ενός χαρτοφυλακίου από το μέσο όρο του. Εν ολίγοις, καθορίζει τον συνολικό κίνδυνο του χαρτοφυλακίου. Μπορεί να προκύψει βάσει ενός σταθμισμένου μέσου όρου ατομικής διακύμανσης και αμοιβαίας συνδιακύμανσης.
Τύπος παραλλαγής χαρτοφυλακίου
Μαθηματικά, ο τύπος διακύμανσης χαρτοφυλακίου που αποτελείται από δύο περιουσιακά στοιχεία παρουσιάζεται ως,
Τύπος παραλλαγής χαρτοφυλακίου = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2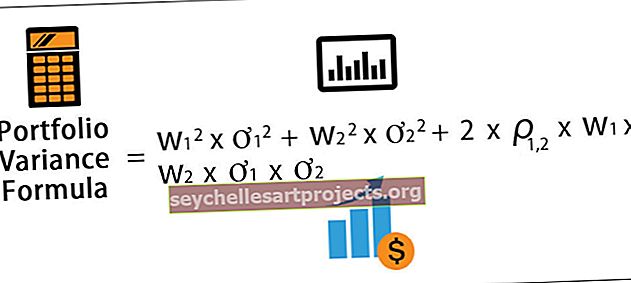
που,
- w i = Βάρος χαρτοφυλακίου περιουσιακού στοιχείου i
- o i 2 = Ατομική διακύμανση του Ι ενεργητικού
- ρ i, j = Συσχέτιση μεταξύ περιουσιακού στοιχείου i και περιουσιακού στοιχείου j
Και πάλι, η διακύμανση μπορεί να επεκταθεί περαιτέρω σε ένα χαρτοφυλάκιο με περισσότερα όχι. περιουσιακών στοιχείων, για παράδειγμα, ένα χαρτοφυλάκιο 3 περιουσιακών στοιχείων μπορεί να αναπαρασταθεί ως,
Τύπος παραλλαγής χαρτοφυλακίου = w 1 2 * ơ 1 2 + w 2 2 * ơ 2 2 + w 3 2 * ơ 3 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2 + 2 * ρ 2,3 * w 2 * w 3 * ơ 2 * ơ 3 + 2 * ρ 3,1 * w 3 * w 1 * ơ 3* ơ 1
Επεξήγηση του Τύπου Παραλλαγής Χαρτοφυλακίου
Ο τύπος διακύμανσης χαρτοφυλακίου ενός συγκεκριμένου χαρτοφυλακίου μπορεί να εξαχθεί χρησιμοποιώντας τα ακόλουθα βήματα:
Βήμα 1: Πρώτον, προσδιορίστε το βάρος κάθε περιουσιακού στοιχείου στο συνολικό χαρτοφυλάκιο και υπολογίζεται διαιρώντας την αξία του περιουσιακού στοιχείου με τη συνολική αξία του χαρτοφυλακίου. Το βάρος του ith περιουσιακού στοιχείου δηλώνεται με το w i .
Βήμα 2: Στη συνέχεια, προσδιορίστε την τυπική απόκλιση κάθε στοιχείου και υπολογίζεται με βάση τη μέση και την πραγματική απόδοση κάθε στοιχείου. Η τυπική απόκλιση του ith περιουσιακού στοιχείου δηλώνεται με ơ i . Το τετράγωνο της τυπικής απόκλισης είναι διακύμανση δηλαδή ơ i 2.
Βήμα 3: Στη συνέχεια, προσδιορίστε τη συσχέτιση μεταξύ των περιουσιακών στοιχείων και καταγράφει βασικά την κίνηση κάθε περιουσιακού στοιχείου σε σχέση με ένα άλλο στοιχείο. Η συσχέτιση δηλώνεται με ρ.
Βήμα 4: Τέλος, ο τύπος διακύμανσης χαρτοφυλακίου δύο στοιχείων προέρχεται βάσει ενός σταθμισμένου μέσου όρου ατομικής διακύμανσης και αμοιβαίας συνδιακύμανσης όπως φαίνεται παρακάτω.
Τύπος παραλλαγής χαρτοφυλακίου = w 1 * ơ 1 2 + w 2 * ơ 2 2 + 2 * ρ 1,2 * w 1 * w 2 * ơ 1 * ơ 2
Παράδειγμα φόρμουλας παραλλαγής χαρτοφυλακίου (με πρότυπο Excel)
Μπορείτε να κατεβάσετε αυτό το Πρότυπο Formula Variance Formula Excel εδώ - Πρότυπο Formula Variance Excel Formula
Ας πάρουμε το παράδειγμα ενός χαρτοφυλακίου που αποτελείται από δύο μετοχές. Η αξία του αποθέματος Α είναι 60.000 $ και η τυπική απόκλιση είναι 15%, ενώ η τιμή του αποθέματος Β είναι 90.000 $ και η τυπική απόκλιση είναι 10%. Υπάρχει συσχέτιση 0,85 μεταξύ των δύο αποθεμάτων. Προσδιορίστε τη διακύμανση.
Δεδομένος,
- Η τυπική απόκλιση του αποθέματος A, ơ A = 15%
- Η τυπική απόκλιση του αποθέματος B, ơ B = 10%
Συσχέτιση, ρ A, B = 0,85
Ακολουθούν δεδομένα για τον υπολογισμό της διακύμανσης χαρτοφυλακίου δύο μετοχών.

Βάρος αποθεμάτων A, w A = 60.000 $ / (60.000 $ + 90.000 $) * 100%

Βάρος αποθεμάτων A = 40% ή 0,40
Βάρος αποθεμάτων B, w B = 90.000 $ / (60.000 $ + 90.000 $) * 100%

Βάρος αποθεμάτων B = 60% ή 0,60
Επομένως, ο υπολογισμός διακύμανσης χαρτοφυλακίου θα έχει ως εξής

Διακύμανση = w A 2 * ơ A 2 + w B 2 * ơ B 2 + 2 * ρ A, B * w A * w B * ơ A * ơ B
= 0,4 ^ 2 * (0,15) 2 + 0,6 ^ 2 * (0,10) 2 + 2 * 0,85 * 0,4 * 0,6 * 0,15 * 0,10

Επομένως, η διακύμανση είναι 1,33%.
Συνάφεια και χρήση
Ένα από τα πιο εντυπωσιακά χαρακτηριστικά του portfolio είναι το γεγονός ότι η αξία του προκύπτει βάσει του σταθμισμένου μέσου όρου των μεμονωμένων διακυμάνσεων καθενός από τα περιουσιακά στοιχεία που προσαρμόζονται από τις συντελεστές τους. Αυτό δείχνει ότι η συνολική διακύμανση είναι μικρότερη από έναν απλό σταθμισμένο μέσο όρο των μεμονωμένων διακυμάνσεων κάθε μετοχής στο χαρτοφυλάκιο. Πρέπει να σημειωθεί ότι ένα χαρτοφυλάκιο με τίτλους που έχουν χαμηλότερη συσχέτιση μεταξύ τους, καταλήγει σε χαμηλότερη διακύμανση χαρτοφυλακίου.
Η κατανόηση του τύπου διαφοροποίησης χαρτοφυλακίου είναι επίσης σημαντική καθώς βρίσκει εφαρμογή στη Σύγχρονη Θεωρία Χαρτοφυλακίου που βασίζεται στη βασική υπόθεση ότι οι κανονικοί επενδυτές σκοπεύουν να μεγιστοποιήσουν τις αποδόσεις τους ελαχιστοποιώντας τον κίνδυνο, όπως η διακύμανση. Ένας επενδυτής συνήθως επιδιώκει αυτό που ονομάζεται αποτελεσματικό όριο και είναι το χαμηλότερο επίπεδο κινδύνου ή μεταβλητότητας στο οποίο ο επενδυτής μπορεί να επιτύχει την απόδοση-στόχο. Τις περισσότερες φορές, οι επενδυτές επενδύουν σε μη συσχετισμένα περιουσιακά στοιχεία για να μειώσουν τον κίνδυνο σύμφωνα με τη Σύγχρονη Θεωρία Χαρτοφυλακίου.
Υπάρχουν περιπτώσεις όπου τα περιουσιακά στοιχεία που ενδέχεται να είναι επικίνδυνα μεμονωμένα μπορούν τελικά να μειώσουν τη διακύμανση ενός χαρτοφυλακίου επειδή μια τέτοια επένδυση είναι πιθανό να αυξηθεί όταν πέσουν άλλες επενδύσεις. Ως εκ τούτου, αυτός ο μειωμένος συσχετισμός μπορεί να βοηθήσει στη μείωση της διακύμανσης ενός υποθετικού χαρτοφυλακίου. Συνήθως, το επίπεδο κινδύνου ενός χαρτοφυλακίου μετριέται χρησιμοποιώντας την τυπική απόκλιση, η οποία υπολογίζεται ως η τετραγωνική ρίζα της διακύμανσης. Η διακύμανση αναμένεται να παραμείνει υψηλή όταν τα σημεία δεδομένων απέχουν πολύ από το μέσο όρο, το οποίο τελικά οδηγεί σε υψηλότερο συνολικό επίπεδο κινδύνου στο χαρτοφυλάκιο.