seychellesartprojects.org

Τύπος για τον προσδιορισμό του μεγέθους του δείγματος του πληθυσμού

Ο τύπος δείγματος μεγέθους βοηθά στον υπολογισμό ή τον καθορισμό του ελάχιστου μεγέθους δείγματος που απαιτείται για να γνωρίζουμε την επαρκή ή σωστή αναλογία του πληθυσμού μαζί με το επίπεδο εμπιστοσύνης και το περιθώριο σφάλματος.

Ο όρος «δείγμα» αναφέρεται στο τμήμα του πληθυσμού που μας επιτρέπει να αντλήσουμε συμπεράσματα σχετικά με τον πληθυσμό και, επομένως, είναι σημαντικό το μέγεθος του δείγματος να είναι επαρκές ώστε να μπορούν να γίνουν ουσιαστικά συμπεράσματα. Με άλλα λόγια, είναι το ελάχιστο μέγεθος που απαιτείται για την εκτίμηση του πραγματικού ποσοστού πληθυσμού με το απαιτούμενο περιθώριο σφάλματος και το επίπεδο εμπιστοσύνης. Ως εκ τούτου, ο προσδιορισμός του κατάλληλου μεγέθους δείγματος είναι ένα από τα επαναλαμβανόμενα προβλήματα στη στατιστική ανάλυση. Η εξίσωση μπορεί να προκύψει χρησιμοποιώντας το μέγεθος του πληθυσμού, την κρίσιμη τιμή της κανονικής κατανομής, την αναλογία δείγματος και το περιθώριο σφάλματος.

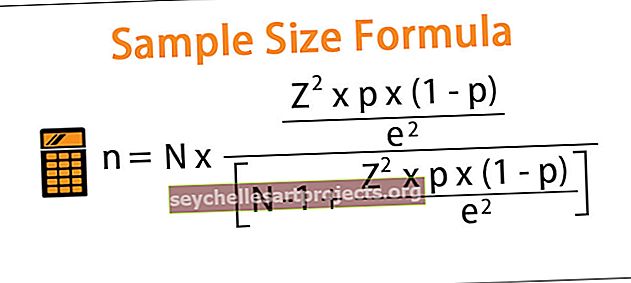
που,

• N = Μέγεθος πληθυσμού,
• Z = Κρίσιμη τιμή της κανονικής κατανομής στο απαιτούμενο επίπεδο εμπιστοσύνης,
• p = Αναλογία δείγματος,
• e = Περιθώριο σφάλματος

Πώς να υπολογίσετε το μέγεθος του δείγματος; (Βήμα βήμα)

• Βήμα 1: Πρώτον, προσδιορίστε το μέγεθος του πληθυσμού που είναι ο συνολικός αριθμός των διακριτών οντοτήτων στον πληθυσμό σας και δηλώνεται με το Ν. [Σημείωση: Σε περίπτωση που το μέγεθος του πληθυσμού είναι πολύ μεγάλο, αλλά ο ακριβής αριθμός δεν είναι γνωστός, τότε χρησιμοποιήστε 100.000 επειδή το μέγεθος του δείγματος δεν αλλάζει πολύ για πληθυσμούς μεγαλύτερους από αυτό.]
• Βήμα 2: Στη συνέχεια, προσδιορίστε την κρίσιμη τιμή της κανονικής κατανομής στο απαιτούμενο επίπεδο εμπιστοσύνης. Για παράδειγμα, η κρίσιμη τιμή στο επίπεδο εμπιστοσύνης 95% είναι 1,96.
• Βήμα 3: Στη συνέχεια, προσδιορίστε την αναλογία δείγματος που μπορεί να χρησιμοποιηθεί από τα προηγούμενα αποτελέσματα της έρευνας ή να συλλεχθεί εκτελώντας μια μικρή πιλοτική έρευνα. [Σημείωση: εάν δεν είστε σίγουροι, μπορεί πάντα να χρησιμοποιήσει το 0,5 ως συντηρητική προσέγγιση και θα δώσει το μεγαλύτερο δυνατό μέγεθος δείγματος.]
• Βήμα 4: Στη συνέχεια, προσδιορίστε το περιθώριο σφάλματος που είναι το εύρος στο οποίο αναμένεται να βρίσκεται ο πραγματικός πληθυσμός . [Σημείωση: Όσο μικρότερο είναι το περιθώριο σφάλματος, τόσο μεγαλύτερη είναι η ακρίβεια και ως εκ τούτου η ακριβής απάντηση.]
• Βήμα 5: Τέλος, η εξίσωση μεγέθους δείγματος μπορεί να εξαχθεί χρησιμοποιώντας το μέγεθος του πληθυσμού (βήμα 1), την κρίσιμη τιμή της κανονικής κατανομής στο απαιτούμενο επίπεδο εμπιστοσύνης (βήμα 2), την αναλογία δείγματος (βήμα 3) και το περιθώριο σφάλματος (βήμα 4) όπως φαίνεται παρακάτω.

Παραδείγματα

Μπορείτε να κατεβάσετε αυτό το πρότυπο δείγματος μεγέθους δείγματος Excel εδώ - Πρότυπο δείγματος μεγέθους δείγματος Excel

Παράδειγμα # 1

Ας πάρουμε το παράδειγμα ενός λιανοπωλητή που ενδιαφέρεται να μάθει πόσοι από τους πελάτες τους αγόρασαν ένα αντικείμενο από αυτούς αφού είδαν τον ιστότοπό τους σε μια συγκεκριμένη ημέρα. Δεδομένου ότι ο ιστότοπός τους έχει κατά μέσο όρο 10.000 προβολές ανά ημέρα, προσδιορίστε το μέγεθος δείγματος των πελατών που πρέπει να παρακολουθούν σε επίπεδο εμπιστοσύνης 95% με περιθώριο σφάλματος 5% εάν:

• Δεν είναι σίγουροι για το τρέχον ποσοστό μετατροπών.
• Γνωρίζουν από προηγούμενες έρευνες ότι το ποσοστό μετατροπής είναι 5%.

Δεδομένος,

• Μέγεθος πληθυσμού, N = 10.000
• Κρίσιμη τιμή σε επίπεδο εμπιστοσύνης 95%, Z = 1,96
•  Περιθώριο σφάλματος, e = 5% ή 0,05

1 - Επειδή το τρέχον ποσοστό μετατροπών είναι άγνωστο, ας υποθέσουμε ότι p = 0,5

Επομένως, το μέγεθος του δείγματος μπορεί να υπολογιστεί χρησιμοποιώντας τον τύπο ως,

= (10.000 * (1,96 2) * 0,5 * (1-0,5) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,5 * (1-0,5) / (0,05 2))))

Ως εκ τούτου, 370 πελάτες θα είναι επαρκείς για την εξαγωγή σημαντικών συμπερασμάτων.

2 - Το τρέχον ποσοστό μετατροπής είναι p = 5% ή 0,05

Επομένως, το μέγεθος του δείγματος μπορεί να υπολογιστεί χρησιμοποιώντας τον παραπάνω τύπο ως,

= (10.000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (10000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Επομένως, ένα μέγεθος 72 πελατών θα είναι επαρκές για την εξαγωγή ουσιαστικών συμπερασμάτων σε αυτήν την περίπτωση.

Παράδειγμα # 2

Ας πάρουμε το παραπάνω παράδειγμα και σε αυτήν την περίπτωση ας υποθέσουμε ότι το μέγεθος του πληθυσμού, δηλαδή η ημερήσια προβολή ιστοτόπου, είναι μεταξύ 100.000 και 120.000, αλλά τότε η ακριβής τιμή δεν είναι γνωστή. Οι υπόλοιπες τιμές είναι ίδιες μαζί με ποσοστό μετατροπής 5%. Υπολογίστε το μέγεθος του δείγματος για 100.000 και 120.000.

Δεδομένος,

• Αναλογία δείγματος, p = 0,05
• Κρίσιμη τιμή σε επίπεδο εμπιστοσύνης 95%, Z = 1,96
•  Περιθώριο σφάλματος, e = 0,05

Επομένως, το μέγεθος δείγματος για N = 100.000 μπορεί να υπολογιστεί ως,

= (100000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (100000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Επομένως, το μέγεθος δείγματος για N = 120.000 μπορεί να υπολογιστεί ως,

= (120000 * (1,96 2) * 0,05 * (1-0,05) / (0,05 2) / (120000 - 1 + ((1,96 2) * 0,05 * (1-0,05) / (0,05 2))))

Επομένως, αποδεικνύεται ότι καθώς το μέγεθος του πληθυσμού αυξάνεται να είναι πολύ μεγάλο, καθίσταται άσχετο με τον υπολογισμό του μεγέθους του δείγματος.

Συνάφεια και χρήσεις

Ο υπολογισμός του μεγέθους δείγματος είναι σημαντικός για την κατανόηση της έννοιας του κατάλληλου μεγέθους δείγματος, επειδή χρησιμοποιείται για την εγκυρότητα των ερευνητικών ευρημάτων. Σε περίπτωση που είναι πολύ μικρό, δεν θα αποδώσει έγκυρα αποτελέσματα, ενώ ένα δείγμα είναι πολύ μεγάλο μπορεί να είναι χάσιμο χρημάτων και χρόνου. Στατιστικά, το σημαντικό μέγεθος δείγματος χρησιμοποιείται κυρίως για έρευνες έρευνας αγοράς, έρευνες υγειονομικής περίθαλψης και έρευνες εκπαίδευσης.