seychellesartprojects.org

Τύπος για τον υπολογισμό του μέσου όρου

Ο μέσος όρος είναι η τιμή που χρησιμοποιείται για την αναπαράσταση του συνόλου των τιμών δεδομένων όπως και ο μέσος όρος που υπολογίζεται από ολόκληρα δεδομένα και αυτός ο τύπος υπολογίζεται προσθέτοντας όλες τις τιμές του συνόλου που δίνεται, που υποδηλώνεται με άθροισμα του Χ και διαιρώντας το με τον αριθμό τιμές που δίνονται σε σύνολο που υποδηλώνονται από το Ν.

Μέσος όρος = (a ₁ + a ₂ +…. + _{A n} ) / n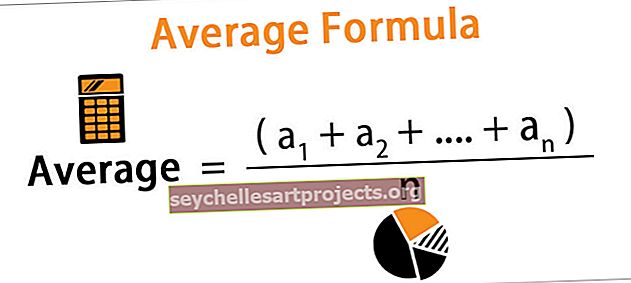

• όπου μια παρατήρηση _i = ith
• n = Αριθμός παρατηρήσεων

Εξήγηση

Ο υπολογισμός του μέσου όρου μπορεί να υπολογιστεί χρησιμοποιώντας τα ακόλουθα βήματα:

• Βήμα 1: Πρώτον, προσδιορίστε την παρατήρηση και συμβολίζονται με ₁ , ₂ ,… .., _{n που} αντιστοιχεί στην 1η παρατήρηση, 2η παρατήρηση,….
• Βήμα 2: Στη συνέχεια, προσδιορίστε τον αριθμό των παρατηρήσεων και συμβολίζεται με το n.
• Βήμα 3: Τέλος, ο μέσος όρος υπολογίζεται προσθέτοντας όλες τις παρατηρήσεις και στη συνέχεια διαιρέστε το αποτέλεσμα με τον αριθμό των παρατηρήσεων όπως φαίνεται παρακάτω.

Μέσος όρος = (a ₁ + a ₂ +…. + _{A n} ) / n

Παραδείγματα

Μπορείτε να πραγματοποιήσετε λήψη αυτού του μέσου προτύπου Formula Excel εδώ - Μέσο πρότυπο Formula Excel

Παράδειγμα # 1

Ας πάρουμε ένα παράδειγμα του John που εγγράφηκε στο πρόγραμμα αποφοίτησης της περιβαλλοντικής επιστήμης. Το τριετές πρόγραμμα σπουδών χωρίζεται σε έξι εξάμηνα και το τελικό μέσο ποσοστό υπολογίζεται με βάση τα ποσοστά που σημειώθηκαν σε όλα τα εξάμηνα. Υπολογίστε το τελικό ποσοστό του John με βάση την ακόλουθη βαθμολογία του:

Παρακάτω δίνονται δεδομένα για τον υπολογισμό του μέσου ποσοστού.

Δεδομένος,

a ₁ = 79%, ₂ = 81%, ₃ = 74%, ₄ = 70%, ₅ = 82%, ₆ = 85%, n = 6

Χρησιμοποιώντας τις παραπάνω πληροφορίες, ο υπολογισμός του μέσου όρου θα έχει ως εξής,

•   Μέσος όρος = (79% + 81% + 74% + 70% + 82% + 85%) / 6

Ο μέσος όρος θα είναι -

• Μέσος όρος = 78,50%

Ως εκ τούτου, ο David σημείωσε ένα τελικό ποσοστό 78,5% στο πρόγραμμα αποφοίτησης.

Χρήσεις

Όπως υποδηλώνει το όνομα «μέσος όρος», αναφέρεται στο κεντρικό σημείο ανάμεσα σε ένα σύνολο παρατηρήσεων και όταν χρησιμοποιείται στον τομέα των μαθηματικών αντιπροσωπεύει τον αριθμό που είναι συνήθως μέσος όρος μιας ομάδας αριθμών. Ο όρος χρησιμοποιείται συχνά για να εκφράσει έναν αριθμό που είναι η αναπαράσταση για μια ομάδα ανθρώπων ή πράγματα. Είναι πολύ σημαντικό διότι βοηθά στη σύνοψη ενός μεγάλου αριθμού δεδομένων σε μία μόνο τιμή και δείχνει επίσης ότι υπάρχει κάποια ασυνέπεια γύρω από την ενιαία τιμή στα αρχικά δεδομένα που αποτελεί ένα πολύ κρίσιμο μέρος της θεωρίας της κεντρικής τάσης.