seychellesartprojects.org

Ορισμός της μεθόδου παλινδρόμησης Least Squares

Μια μέθοδος παλινδρόμησης ελάχιστων τετραγώνων είναι μια μορφή ανάλυσης παλινδρόμησης που καθιερώνει τη σχέση μεταξύ της εξαρτώμενης και της ανεξάρτητης μεταβλητής μαζί με μια γραμμική γραμμή. Αυτή η γραμμή αναφέρεται ως «γραμμή βέλτιστης εφαρμογής».

Η ανάλυση παλινδρόμησης είναι μια στατιστική μέθοδος με τη βοήθεια της οποίας μπορεί κανείς να εκτιμήσει ή να προβλέψει τις άγνωστες τιμές μιας μεταβλητής από τις γνωστές τιμές μιας άλλης μεταβλητής. Η μεταβλητή που χρησιμοποιείται για την πρόβλεψη της μεταβλητής ενδιαφέροντος ονομάζεται ανεξάρτητη ή επεξηγηματική μεταβλητή και η μεταβλητή που προβλέπεται είναι η εξαρτημένη ή εξηγούμενη μεταβλητή.

Ας εξετάσουμε δύο μεταβλητές x & y. Αυτά απεικονίζονται σε ένα γράφημα με τιμές x σε τιμές αξόνων x του y στον άξονα y. Αυτές οι τιμές αντιπροσωπεύονται από τις τελείες στο παρακάτω γράφημα. Μια ευθεία γραμμή σχεδιάζεται μέσα από τις τελείες - αναφέρεται ως η γραμμή της καλύτερης εφαρμογής.

Ο στόχος της παλινδρόμησης των τετραγώνων είναι να διασφαλιστεί ότι η γραμμή που σχεδιάζεται μέσω του συνόλου των παρεχόμενων τιμών δημιουργεί τη στενότερη σχέση μεταξύ των τιμών.

Φόρμουλα παλινδρόμησης Least Squares

Η γραμμή παλινδρόμησης με τη μέθοδο Least Squares υπολογίζεται χρησιμοποιώντας τον ακόλουθο τύπο -

ŷ = a + bx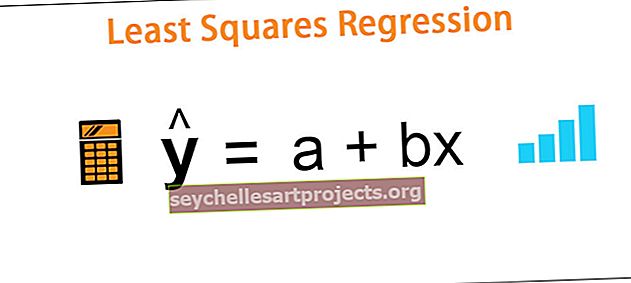

Που,

• dependent = εξαρτημένη μεταβλητή
• x = ανεξάρτητη μεταβλητή
• a = y-τομή
• b = κλίση της γραμμής

Η κλίση της γραμμής b υπολογίζεται χρησιμοποιώντας τον ακόλουθο τύπο -

Ή

Το Y-intercept, το «a» υπολογίζεται χρησιμοποιώντας τον ακόλουθο τύπο -

Γραμμή Best Fit στο Least Square Regression

Η γραμμή βέλτιστης εφαρμογής είναι μια ευθεία γραμμή που σχηματίζεται μέσω μιας διασποράς σημείων δεδομένων που αντιπροσωπεύει καλύτερα τη σχέση μεταξύ τους.

Ας εξετάσουμε το ακόλουθο γράφημα όπου ένα σύνολο δεδομένων απεικονίζεται κατά μήκος του άξονα x και y. Αυτά τα σημεία δεδομένων απεικονίζονται χρησιμοποιώντας τις μπλε κουκκίδες. Τρεις γραμμές σχεδιάζονται μέσω αυτών των σημείων - μια πράσινη, μια κόκκινη και μια μπλε γραμμή. Η πράσινη γραμμή περνά από ένα μόνο σημείο και η κόκκινη γραμμή περνά από τρία σημεία δεδομένων. Ωστόσο, η μπλε γραμμή διέρχεται από τέσσερα σημεία δεδομένων και η απόσταση μεταξύ των υπολειπόμενων σημείων προς την μπλε γραμμή είναι ελάχιστη σε σύγκριση με τις άλλες δύο γραμμές.

Στο παραπάνω γράφημα, η μπλε γραμμή αντιπροσωπεύει τη γραμμή της καλύτερης εφαρμογής, καθώς βρίσκεται πλησιέστερα σε όλες τις τιμές και η απόσταση μεταξύ των σημείων έξω από τη γραμμή προς τη γραμμή είναι ελάχιστη (δηλαδή η απόσταση μεταξύ των υπολειμμάτων έως τη γραμμή της καλύτερης εφαρμογής - αναφέρεται επίσης ως άθροισμα τετραγώνων υπολειμμάτων). Στις άλλες δύο γραμμές, το πορτοκαλί και το πράσινο, η απόσταση μεταξύ των υπολειμμάτων προς τις γραμμές είναι μεγαλύτερη σε σύγκριση με την μπλε γραμμή.

Η μέθοδος των λιγότερων τετραγώνων παρέχει τη στενότερη σχέση μεταξύ των εξαρτώμενων και ανεξάρτητων μεταβλητών ελαχιστοποιώντας την απόσταση μεταξύ των υπολειμμάτων και της γραμμής της βέλτιστης εφαρμογής, δηλαδή το άθροισμα των τετραγώνων των υπολειμμάτων είναι ελάχιστο υπό αυτήν την προσέγγιση. Εξ ου και ο όρος «λιγότερα τετράγωνα».

Παραδείγματα γραμμής παλινδρόμησης Least Squares

Ας εφαρμόσουμε αυτούς τους τύπους στην παρακάτω ερώτηση -

Μπορείτε να κατεβάσετε αυτό το Πρότυπο Regression Excel Least Squares εδώ - Πρότυπο Legr Squad Regression Excel

Παράδειγμα # 1

Οι λεπτομέρειες σχετικά με την εμπειρία των τεχνικών σε μια εταιρεία (σε αρκετά χρόνια) και τη βαθμολογία απόδοσής τους παρέχονται στον παρακάτω πίνακα. Χρησιμοποιώντας αυτές τις τιμές, εκτιμήστε την απόδοση για έναν τεχνικό με 20 χρόνια εμπειρίας.

Λύση -

Για να υπολογίσουμε πρώτα τα λιγότερα τετράγωνα, θα υπολογίσουμε την αναχαίτιση Υ (α) και την κλίση μιας γραμμής (β) ως εξής -

Η κλίση της γραμμής (β)

• b = 6727 - [(80 * 648) / 8] / 1018 - [(80) 2/8]
• = 247/218
• = 1.13

Υ-τομή (α)

• a = 648 - (1,13) (80) / 8
• = 69.7

Η γραμμή παλινδρόμησης υπολογίζεται ως εξής -

Αντικατάσταση 20 για την τιμή του x στον τύπο,

• ŷ = a + bx
• ŷ = 69,7 + (1,13) (20)
• 92 = 92.3

Η βαθμολογία απόδοσης για έναν τεχνικό με 20 χρόνια εμπειρίας εκτιμάται ότι είναι 92,3.

Παράδειγμα # 2

Εξίσωση παλινδρόμησης Least Squares με χρήση του Excel

Η εξίσωση παλινδρόμησης ελάχιστων τετραγώνων μπορεί να υπολογιστεί χρησιμοποιώντας το Excel με τα ακόλουθα βήματα -

• Εισαγωγή πίνακα δεδομένων στο Excel.

• Εισαγάγετε ένα γράφημα διασποράς χρησιμοποιώντας τα σημεία δεδομένων.

• Εισαγάγετε μια γραμμή τάσης στο γράφημα διασποράς.

• Στις επιλογές γραμμής τάσης - επιλέξτε γραμμική γραμμή τάσης και επιλέξτε εξίσωση οθόνης στο γράφημα.

• Η εξίσωση παλινδρόμησης ελάχιστων τετραγώνων για το δεδομένο σύνολο δεδομένων excel εμφανίζεται στο γράφημα.

Έτσι, υπολογίζεται η εξίσωση παλινδρόμησης ελάχιστων τετραγώνων για το δεδομένο σύνολο δεδομένων excel. Χρησιμοποιώντας την εξίσωση, μπορούν να γίνουν προβλέψεις και αναλύσεις τάσεων. Τα εργαλεία του Excel παρέχουν επίσης λεπτομερείς υπολογισμούς παλινδρόμησης.

Πλεονεκτήματα

• Η μέθοδος ανάλυσης παλινδρόμησης με λιγότερα τετράγωνα είναι πιο κατάλληλη για μοντέλα πρόβλεψης και ανάλυση τάσεων. Χρησιμοποιείται καλύτερα στους τομείς των οικονομικών, των χρηματοοικονομικών και των χρηματιστηριακών αγορών, όπου η αξία οποιασδήποτε μελλοντικής μεταβλητής προβλέπεται με τη βοήθεια των υπαρχουσών μεταβλητών και τη σχέση μεταξύ τους.
• Η μέθοδος λιγότερων τετραγώνων παρέχει τη στενότερη σχέση μεταξύ των μεταβλητών. Η διαφορά μεταξύ των αθροισμάτων των τετραγώνων υπολειμμάτων στη γραμμή της καλύτερης εφαρμογής είναι ελάχιστη με αυτήν τη μέθοδο.
• Ο υπολογισμός είναι απλός και εύχρηστος.

Μειονεκτήματα

• Η μέθοδος λιγότερων τετραγώνων βασίζεται στον καθορισμό της στενότερης σχέσης μεταξύ ενός δεδομένου συνόλου μεταβλητών. Ο υπολογισμός είναι ευαίσθητος στα δεδομένα και σε περίπτωση οποιωνδήποτε ακραίων τιμών (εξαιρετικά δεδομένα), τα αποτελέσματα ενδέχεται να επηρεάσουν σημαντικά
• Αυτός ο τύπος υπολογισμού ταιριάζει καλύτερα στα γραμμικά μοντέλα. Για μη γραμμικές εξισώσεις, εφαρμόζονται πιο εξαντλητικοί μηχανισμοί υπολογισμού.

συμπέρασμα

Η μέθοδος λιγότερων τετραγώνων είναι μια από τις πιο δημοφιλείς μεθόδους για μοντέλα πρόβλεψης και ανάλυση τάσεων. Όταν υπολογίζεται κατάλληλα, παρέχει τα καλύτερα αποτελέσματα.