Τύπος επιστροφής χαρτοφυλακίου | Υπολογίστε την απόδοση του συνολικού χαρτοφυλακίου

Τύπος επιστροφής χαρτοφυλακίου | Υπολογίστε την απόδοση του συνολικού χαρτοφυλακίου | Παράδειγμα

Τύπος για τον υπολογισμό της απόδοσης του συνολικού χαρτοφυλακίου

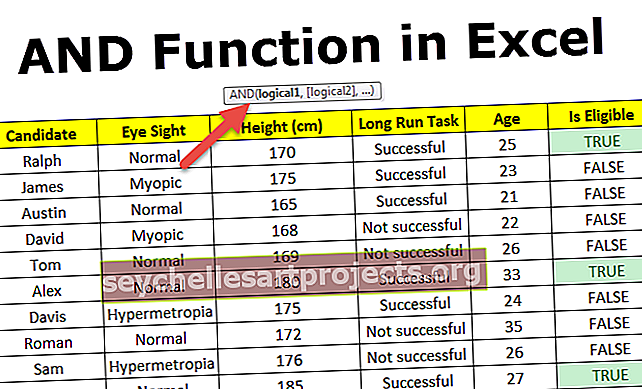
Ο τύπος επιστροφής χαρτοφυλακίου χρησιμοποιείται για τον υπολογισμό της απόδοσης του συνολικού χαρτοφυλακίου που αποτελείται από τα διαφορετικά μεμονωμένα περιουσιακά στοιχεία, όπου σύμφωνα με τον τύπο, η απόδοση χαρτοφυλακίου υπολογίζεται με τον υπολογισμό της απόδοσης επένδυσης που αποκτήθηκε σε μεμονωμένο περιουσιακό στοιχείο πολλαπλασιασμένο με την αντίστοιχη κατηγορία βάρους στο συνολικό χαρτοφυλάκιο και προσθέτοντας όλα τα αποτελέσματα μαζί.

Η απόδοση χαρτοφυλακίου μπορεί να οριστεί ως το άθροισμα του προϊόντος των αποδόσεων επένδυσης που κερδίζονται στο μεμονωμένο περιουσιακό στοιχείο με την κατηγορία βάρους αυτού του μεμονωμένου περιουσιακού στοιχείου σε ολόκληρο το χαρτοφυλάκιο. Αντιπροσωπεύει μια απόδοση στο χαρτοφυλάκιο και όχι μόνο σε ένα μεμονωμένο περιουσιακό στοιχείο.

Η αναμενόμενη απόδοση μπορεί να υπολογιστεί με ένα προϊόν πιθανών αποτελεσμάτων (δηλ. Αποδόσεις που αντιπροσωπεύονται από το r παρακάτω) από τα βάρη κάθε περιουσιακού στοιχείου στο χαρτοφυλάκιο (δηλ. Αντιπροσωπεύεται από το w) και μετά από αυτόν τον υπολογισμό του αθροίσματος αυτών των αποτελεσμάτων.

R _p = in _{i = 1} w _i r _i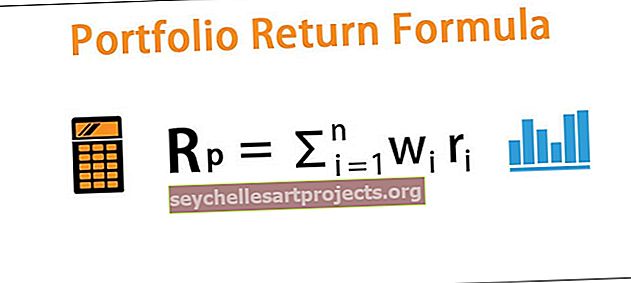

Όπου in _{i = 1} w _i = 1

w είναι το βάρος κάθε περιουσιακού στοιχείου
r είναι η απόδοση ενός περιουσιακού στοιχείου

Υπολογισμός επιστροφής χαρτοφυλακίου (βήμα προς βήμα)

Ο υπολογισμός της απόδοσης χαρτοφυλακίου είναι αρκετά απλός αλλά απαιτεί λίγη προσοχή.

Βήμα 1: Λάβετε την ατομική απόδοση περιουσιακών στοιχείων στην οποία έχουν επενδυθεί τα κεφάλαια. Για παράδειγμα, εάν ένας επενδυτής έχει επενδύσει σε ίδια κεφάλαια, πρέπει να υπολογίσει ολόκληρη την απόδοση που είναι η συνολική απόδοση, συμπεριλαμβανομένων των ενδιάμεσων ταμειακών ροών που σε περίπτωση μετοχών θα ήταν μέρισμα.
Βήμα 2: Υπολογίστε τα βάρη του μεμονωμένου περιουσιακού στοιχείου στο οποίο επενδύονται τα κεφάλαια. Αυτό μπορεί να γίνει διαιρώντας το επενδυμένο ποσό αυτού του περιουσιακού στοιχείου με το συνολικό επενδυμένο κεφάλαιο.
Βήμα 3: Πάρτε το προϊόν της επιστροφής που υπολογίζεται στο βήμα 1 με το βάρος που υπολογίζεται στο βήμα 2.
Βήμα 4: Το τρίτο βήμα θα επαναληφθεί έως ότου ολοκληρωθούν οι υπολογισμοί όλων των στοιχείων. Τελικά, τέλος, πρέπει να προσθέσουμε το προϊόν όλων των μεμονωμένων αποδόσεων περιουσιακών στοιχείων με βάση την κατηγορία βάρους που θα είναι η απόδοση χαρτοφυλακίου.

Παραδείγματα

Μπορείτε να κάνετε λήψη αυτού του προτύπου Excel Formula Return Formula εδώ - Πρότυπο επιστροφής χαρτοφυλακίου Excel

Παράδειγμα # 1

Σκεφτείτε την ABC ltd ότι μια εταιρεία διαχείρισης περιουσιακών στοιχείων έχει επενδύσει σε 2 διαφορετικά περιουσιακά στοιχεία μαζί με την απόδοση που κέρδισε πέρυσι. Πρέπει να κερδίσετε μια απόδοση χαρτοφυλακίου.

Λύση:

Μας δίνεται η μεμονωμένη απόδοση περιουσιακών στοιχείων και μαζί με αυτό το ποσό επένδυσης, επομένως πρώτα θα ανακαλύψουμε τα βάρη ως εξής,

Βάρος (Κατηγορία ενεργητικού 1) = 1,00,000,00 / 1,50,000,00 = 0,67

Ομοίως, έχουμε υπολογίσει το βάρος της κατηγορίας ενεργητικού 2

Βάρος (Κατηγορία ενεργητικού 1) = 50.000,00 / 1,50,000.00 = 0,33

Τώρα για τον υπολογισμό της απόδοσης χαρτοφυλακίου, πρέπει να πολλαπλασιάσουμε τα βάρη με την απόδοση του περιουσιακού στοιχείου και στη συνέχεια θα συνοψίσουμε αυτές τις αποδόσεις.

W _i R _i (Κατηγορία ενεργητικού 1) = 0,67 * 10% = 6,67%

Ομοίως, έχουμε υπολογίσει το W _i R _i για την κατηγορία 2 Asset

W _i R _i (Κατηγορία ενεργητικού 2) = 0,33 * 11%
= 3,67%

Ο υπολογισμός της απόδοσης χαρτοφυλακίου έχει ως εξής,

Επιστροφή χαρτοφυλακίου

Η απόδοση χαρτοφυλακίου θα είναι 10,33%

Παράδειγμα # 2

Η JP Morgan κυνηγά μια από τις μεγαλύτερες επενδυτικές τραπεζικές εταιρείες έχει πραγματοποιήσει αρκετές επενδύσεις σε διάφορες κατηγορίες περιουσιακών στοιχείων. Ο κ. Dimon ο πρόεδρος της εταιρείας ενδιαφέρεται να γνωρίζει τις αποδόσεις της συνολικής επένδυσης που πραγματοποιεί η εταιρεία. Πρέπει να υπολογίσετε την απόδοση χαρτοφυλακίου.

Λύση:

Μας δίνεται μόνο η τελευταία αγοραία αξία και δεν δίνεται άμεση απόδοση. Ως εκ τούτου, πρώτα, πρέπει να υπολογίσουμε την απόδοση μεμονωμένων περιουσιακών στοιχείων.

Πρέπει να αφαιρέσουμε το ποσό της επένδυσης από την αγοραία αξία για να φτάσουμε στην υπερβολική απόδοση και, στη συνέχεια, διαιρώντας το ίδιο με το ποσό της επένδυσης, θα αποδώσουμε τις αποδόσεις μας στο μεμονωμένο περιουσιακό στοιχείο.

Σημείωση: Για λεπτομερή υπολογισμό, ανατρέξτε στο πρότυπο excel.

Έχουμε τώρα την ατομική απόδοση περιουσιακών στοιχείων και μαζί με αυτό το ποσό επένδυσης και τώρα θα μάθουμε τα βάρη χρησιμοποιώντας το ποσό της επένδυσης και όχι την αγοραία αξία ως εξής,

Βάρος ιδίων κεφαλαίων = 300000000/335600000 = 0,3966

Ομοίως, υπολογίσαμε το βάρος όλων των άλλων στοιχείων.

Ο υπολογισμός της απόδοσης χαρτοφυλακίου έχει ως εξής,

Επιστροφή χαρτοφυλακίου

Ως εκ τούτου, η απόδοση χαρτοφυλακίου που κέρδισε η JP Morgan είναι 21,57%

Παράδειγμα # 3

Η Gautam είναι ένα άτομο που πρόσφατα άρχισε να επενδύει στην αγορά. Έχει επενδύσει σε μετοχή XYZ για 100.000 και έχει περάσει ένα έτος και έκτοτε έχει λάβει μέρισμα 5.000 και η τρέχουσα αγοραία αξία της μετοχής XYZ διαπραγματεύεται με ασφάλιστρο 10%. Επίσης, έχει επενδύσει σε πάγια κατάθεση για 20.000 και η Τράπεζα παρέχει απόδοση 7% σε αυτήν. Και τέλος, έχει επενδύσει σε γη στην πατρίδα του για 500.000 και η τρέχουσα αγοραία αξία είναι 700.000. Σας πλησίασε για να υπολογίσετε την απόδοση χαρτοφυλακίου.

Λύση:

Σημείωση: Για λεπτομερή υπολογισμό, ανατρέξτε στο πρότυπο excel.

Βάρος (XYZ Stock) = 1,00,000 / 6,20,000 = 0,1613

Ομοίως, έχουμε υπολογίσει το βάρος και για άλλα στοιχεία.

(XYZ Stock) W _i R _i = 0,15 * 0,1613 = 2,42%

Ομοίως, υπολογίσαμε το W _i R _{i και} για άλλα συγκεκριμένα.

Ο υπολογισμός της απόδοσης χαρτοφυλακίου έχει ως εξής,

Επιστροφή χαρτοφυλακίου

Ως εκ τούτου, η απόδοση χαρτοφυλακίου που κέρδισε ο κ. Gautam είναι 35,00%

Συνάφεια και χρήση

Είναι σημαντικό να κατανοήσουμε την έννοια της αναμενόμενης φόρμουλας απόδοσης του χαρτοφυλακίου, καθώς η ίδια θα χρησιμοποιηθεί από αυτούς τους επενδυτές, ώστε να μπορούν να προβλέψουν το κέρδος ή τη ζημία που μπορεί να συμβεί στα κεφάλαια που επενδύουν από αυτούς. Με βάση αυτήν την αναμενόμενη φόρμουλα απόδοσης, ένας επενδυτής μπορεί να λάβει απόφαση σχετικά με την επένδυση σε ένα περιουσιακό στοιχείο, δεδομένης της πιθανής απόδοσής του.

Επιπλέον, ένας επενδυτής θα είναι επίσης σε θέση να αποφασίσει για το βάρος του περιουσιακού στοιχείου σε ένα χαρτοφυλάκιο, δηλαδή ποιο ποσοστό των κεφαλαίων θα πρέπει να επενδυθεί και στη συνέχεια να κάνει την απαιτούμενη αλλαγή.

Επίσης, ένας επενδυτής μπορεί να χρησιμοποιήσει τον τύπο της αναμενόμενης απόδοσης για την κατάταξη του μεμονωμένου περιουσιακού στοιχείου και περαιτέρω μπορεί να επενδύσει τα κεφάλαια ανά κατάταξη και, στη συνέχεια, να τα συμπεριλάβει στο χαρτοφυλάκιό του. Με άλλα λόγια, θα αυξήσει το βάρος αυτής της κατηγορίας περιουσιακών στοιχείων της οποίας η αναμενόμενη απόδοση είναι υψηλότερη.

seychellesartprojects.org