Διασταυρούμενη τιμή ελαστικότητας της ζήτησης (Ορισμός) | Βήμα προς βήμα Ερμηνεία
Διασταυρούμενη τιμή Ελαστικότητα του ορισμού της ζήτησης
Η ελαστικότητα της ζήτησης διασταυρούμενης τιμής μετρά τη σχέση μεταξύ της τιμής μιας ζήτησης, δηλαδή, της αλλαγής της ποσότητας που απαιτείται από ένα προϊόν με τη μεταβολή της τιμής του δεύτερου προϊόντος, όπου εάν και τα δύο προϊόντα είναι υποκατάστατα, θα δείξει μια θετική διασταυρούμενη ελαστικότητα της ζήτησης και εάν και τα δύο είναι συμπληρωματικά αγαθά, θα έδειχνε μια έμμεση ή αρνητική διασταυρούμενη ελαστικότητα της ζήτησης. Με απλούς όρους, μετρά την ευαισθησία της ζήτησης για μία ποσότητα X όταν αλλάζει η τιμή του σχετικού αγαθού Y.
Διασταυρούμενη τιμή ελαστικότητας της ζήτησης
Υπολογίζεται διαιρώντας την ποσοστιαία μεταβολή στην ποσότητα του καλού Χ με την ποσοστιαία μεταβολή στην τιμή του καλού Υ που αντιπροσωπεύεται μαθηματικά ως
Διασταυρούμενη τιμή Ελαστικότητα ζήτησης = (ΔQ X / Q X ) ÷ (ΔP Y / P Y )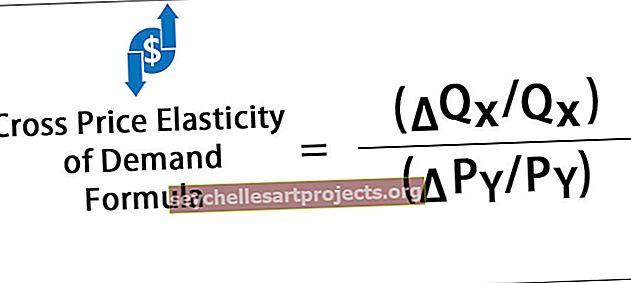
Επιπλέον, μπορεί να εξεταστεί ο τύπος της ελαστικότητας της ζήτησης μεταξύ τιμών
Ελαστικότητα ζήτησης πολλαπλής τιμής = (Q 1X - Q 0X ) / (Q 1X + Q 0X ) ÷ (P 1Y - P 0Y ) / (P 1Y + P 0Y ),που
- Q 0X = Αρχική απαιτούμενη ποσότητα καλής X,
- Q 1X = Τελική απαιτούμενη ποσότητα καλής X,
- P 0Y = Αρχική τιμή των καλών Y και
- P 1Y = Τελική τιμή καλής Υ
Βήμα προς βήμα Υπολογισμός της Ελαστικότητας της Ζήτησης
Αυτό μπορεί να προσδιοριστεί στα ακόλουθα πέντε βήματα:
- Βήμα 1: Αρχικά, προσδιορίστε P 0Y και Q 0X που είναι η αρχική τιμή του αγαθού, μια αρχικά απαιτούμενη ποσότητα καλής X αντίστοιχα.
- Βήμα 2: Τώρα, προσδιορίστε την τελική απαιτούμενη ποσότητα του καλού X και την τελική τιμή του καλής Υ που ορίζονται ως Q 1X και P 1Y αντίστοιχα.
- Βήμα # 3: Τώρα επεξεργαστείτε τον αριθμητή του τύπου που αντιπροσωπεύει την ποσοστιαία αλλαγή στην ποσότητα. Επιτυγχάνεται διαιρώντας τη διαφορά των τελικών και των αρχικών ποσοτήτων (Q 1X - Q 0X ) με άθροισμα των τελικών και των αρχικών ποσοτήτων (Q 1X + Q 0X ) δηλαδή (Q 1X - Q 0X ) / (Q 1X + Q 0X ).
- Βήμα # 4: Τώρα επεξεργαστείτε τον παρονομαστή του τύπου που αντιπροσωπεύει την ποσοστιαία αλλαγή στην τιμή. Επιτυγχάνεται διαιρώντας τη διαφορά των τελικών και των αρχικών τιμών (P 1Y - P 0Y ) με άθροισμα των τελικών και αρχικών τιμών (P 1Y + P 0Y ) δηλαδή (P 1Y - P 0Y ) / (P 1Y + P 0Y ).
- Βήμα # 5: Τέλος, η ελαστικότητα της ζήτησης μεταξύ τιμών υπολογίζεται διαιρώντας την έκφραση στο Βήμα 3 με έκφραση στο Βήμα 4 όπως φαίνεται παρακάτω.
Ελαστικότητα πολλαπλής τιμής της ζήτησης Τύπος = (Q 1X - Q 0X ) / (Q 1X + Q 0X ) ÷ (P 1Y - P 0Y ) / (P 1Y + P 0Y )
Παραδείγματα
Παράδειγμα # 1
Ας πάρουμε το απλό παράδειγμα βενζίνης και επιβατικών οχημάτων. Ας υποθέσουμε, λοιπόν, ότι η αύξηση της τιμής βενζίνης κατά 50% οδήγησε σε μείωση της αγοράς επιβατικών οχημάτων κατά 10%. Υπολογίστε τη διασταυρούμενη ελαστικότητα της ζήτησης σε αυτήν την περίπτωση.
Χρησιμοποιώντας τον παραπάνω τύπο, η ελαστικότητα της ζήτησης μεταξύ τιμών μπορεί να υπολογιστεί ως:
Ποσοστό αλλαγής μετά τον αριθμό των επιβατικών οχημάτων ÷ Το ποσοστό αλλάζει την τιμή της βενζίνης

Δεδομένου ότι μπορούμε να δούμε μια αρνητική τιμή για τη διασταυρούμενη ελαστικότητα της ζήτησης, δικαιώνει τη συμπληρωματική σχέση μεταξύ βενζίνης και επιβατικών οχημάτων.
Παράδειγμα # 2
Ας υποθέσουμε ότι υπάρχουν δύο εταιρείες στην επιχείρηση πώλησης αναψυκτικών. Προς το παρόν, η εταιρεία 2 πωλεί αναψυκτικά Y στα 3,50 $ ανά φιάλη, ενώ η εταιρεία 1 είναι σε θέση να πουλά 4.000 μπουκάλια αναψυκτικών Y την εβδομάδα. Προκειμένου να επηρεαστούν οι πωλήσεις της εταιρείας 1, η εταιρεία 2 αποφασίστηκε να μειώσει την τιμή στα 2,50 $, με αποτέλεσμα τη μείωση των πωλήσεων 3.000 μπουκαλιών αναψυκτικών Y την εβδομάδα. Υπολογίστε τη διασταυρούμενη ελαστικότητα της ζήτησης στην περίπτωση.
Δεδομένου, Q 0X = 4.000 μπουκάλια, Q 1X = 3.000 μπουκάλια, P 0Y = 3.50 $ και P 1Y = 2.50 $
Επομένως, η διασταυρούμενη ελαστικότητα της ζήτησης μπορεί να υπολογιστεί χρησιμοποιώντας τον παραπάνω τύπο ως,
- Διασταυρούμενη ελαστικότητα της ζήτησης = (3.000 - 4.000) / (3.000 + 4.000) ÷ (2,50 $ - 3,50 $) / (2,50 $ + 3,50 $)
- = (-1 / 7) ÷ (-1 / 6)
- = 6/7 ή 0,857
Δεδομένου ότι μπορούμε να δούμε μια θετική τιμή για τη διασταυρούμενη ελαστικότητα της ζήτησης, δικαιώνει την ανταγωνιστική σχέση μεταξύ αναψυκτικών X και αναψυκτικών Y.
Συνάφεια και χρήση
Είναι υψίστης σημασίας για μια επιχείρηση να κατανοήσει την έννοια και τη συνάφεια της ελαστικότητας της ζήτησης μεταξύ τιμών για να κατανοήσει τη σχέση μεταξύ της τιμής ενός αγαθού και της απαιτούμενης ποσότητας ενός άλλου αγαθού σε αυτήν την τιμή. Μπορεί να χρησιμοποιηθεί για τον καθορισμό της τιμολογιακής πολιτικής για διαφορετικές αγορές και για διάφορα προϊόντα ή υπηρεσίες. Η ελαστικότητα διασταυρούμενης τιμής συμπεριφέρεται διαφορετικά με βάση τον τύπο σχέσης μεταξύ των προϊόντων που συζητούνται παρακάτω.
# 1 - Προϊόντα αντικατάστασης
Σε περίπτωση που και τα δύο αγαθά που είναι τέλεια υποκατάστατα το ένα το άλλο οδηγούν σε τέλειο ανταγωνισμό, τότε μια αύξηση στην τιμή μιας καλής θέλησης οδηγεί σε αύξηση της ζήτησης για το ανταγωνιστικό προϊόν. Για παράδειγμα, διάφορες μάρκες δημητριακών είναι παραδείγματα υποκατάστατων προϊόντων. Πρέπει να σημειωθεί ότι η ελαστικότητα μεταξύ δύο τιμών για δύο υποκατάστατα θα είναι θετική.
# 2 - Συμπληρωματικά προϊόντα
Εάν στην περίπτωση που ένα αγαθό είναι συμπληρωματικό του άλλου αγαθού, τότε η μείωση της τιμής μιας καλής θέλησης οδηγεί σε αύξηση της ζήτησης για το συμπληρωματικό αγαθό. Όσο ισχυρότερη είναι η σχέση μεταξύ των δύο προϊόντων, τόσο υψηλότερος θα είναι ο συντελεστής ελαστικότητας της ζήτησης μεταξύ τιμών. Για παράδειγμα, οι κονσόλες παιχνιδιών και τα παιχνίδια λογισμικού είναι παραδείγματα συμπληρωματικών προϊόντων. Πρέπει να σημειωθεί ότι η διασταυρούμενη ελαστικότητα θα είναι αρνητική για συμπληρωματικά προϊόντα.
# 3 - Άσχετα προϊόντα
Σε περίπτωση που δεν υπάρχει σχέση μεταξύ των εμπορευμάτων, η αύξηση της τιμής ενός αγαθού δεν θα επηρεάσει τη ζήτηση για το άλλο προϊόν. Ως τέτοια, τα άσχετα προϊόντα έχουν μηδενική διασταυρούμενη ελαστικότητα. Για παράδειγμα, η επίδραση των αλλαγών στους ναύλους ταξί στη ζήτηση γάλακτος στην αγορά.