seychellesartprojects.org

Ορισμός Sharpe Ratio

Ο λόγος Sharpe είναι ο λόγος που αναπτύχθηκε από τον William F. Sharpe και χρησιμοποιήθηκε από τους επενδυτές για να αποκομίσει την υπερβολική μέση απόδοση του χαρτοφυλακίου έναντι του ποσοστού απόδοσης χωρίς κίνδυνο, ανά μονάδα της μεταβλητότητας (τυπική απόκλιση) του χαρτοφυλακίου.

Εξήγηση

Το Sharpe Ratio είναι ένα κρίσιμο στοιχείο για τη σήμανση των συνολικών αποδόσεων ενός χαρτοφυλακίου. Είναι η μέση απόδοση που κερδίζεται πέρα ​​από την απόδοση χωρίς κίνδυνο σε σύγκριση με το συνολικό ποσό του κινδύνου. Είναι ένας τρόπος να εξεταστεί η απόδοση μιας επένδυσης προσαρμόζοντας το στοιχείο κινδύνου. Η αναλογία Sharpe χαρακτηρίζει πόσο καλά η απόδοση ενός περιουσιακού στοιχείου αποζημιώνει τον επενδυτή για τον κίνδυνο που αναλαμβάνει. Κατά τη σύγκριση δύο περιουσιακών στοιχείων έναντι ενός κοινού κριτηρίου αναφοράς, αυτό που παρέχει υψηλότερη αναλογία Sharpe αναφέρεται ως ευνοϊκή επενδυτική ευκαιρία στο ίδιο επίπεδο κινδύνου.

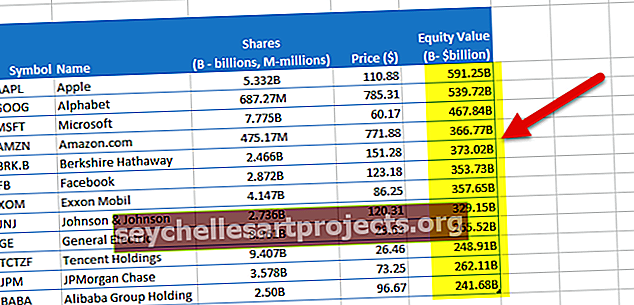
Αν κοιτάξετε τον παραπάνω πίνακα, θα δείτε ότι το PRWCX έχει υψηλότερη αναλογία Sharpe 1,48 και είναι το καλύτερο ταμείο στην ομάδα του.

Το Sharpe Ratio, όπως και κάθε άλλο μαθηματικό μοντέλο, βασίζεται στην ακρίβεια των δεδομένων που πρέπει να είναι σωστά. Κατά την εξέταση της επενδυτικής απόδοσης των περιουσιακών στοιχείων με εξομάλυνση των αποδόσεων, ο λόγος Sharpe θα προέκυπτε από την απόδοση των υποκείμενων περιουσιακών στοιχείων και όχι από τις αποδόσεις του κεφαλαίου. Αυτή η αναλογία μαζί με το Treynor Ratios και το Jeson's Alphas χρησιμοποιούνται συχνά για την κατάταξη της απόδοσης διαφόρων χαρτοφυλακίων ή διαχειριστών κεφαλαίων.

Τύπος

Το 1966, ο William Sharpe ανέπτυξε αυτήν την αναλογία που αρχικά την ονόμαζε ως «ανταμοιβή προς μεταβλητότητα» πριν αρχίσει να ονομάζεται λόγος Sharpe από τους επόμενους ακαδημαϊκούς και χρηματοοικονομικούς φορείς. Ορίστηκε με πολλούς τρόπους έως ότου καταγράφηκε ως εξής:

Τύπος Sharpe Ratio = (Αναμενόμενη απόδοση - Ποσοστό απόδοσης χωρίς κίνδυνο) / Τυπική απόκλιση (Μεταβλητότητα)

Μερικές από τις έννοιες που πρέπει να κατανοήσουμε είναι:

• Επιστροφές - Οι επιστροφές θα μπορούσαν να είναι διαφόρων συχνοτήτων, όπως ημερήσια, εβδομαδιαία, μηνιαία ή ετησίως, εφόσον η διανομή κατανέμεται κανονικά, καθώς αυτές οι αποδόσεις μπορούν να ετησιοποιηθούν για να φτάσουν σε ακριβή αποτελέσματα. Μη φυσιολογικές καταστάσεις όπως υψηλότερες κορυφές, η ασυμμετρία στην κατανομή μπορεί να είναι ένα πρόβλημα περιοχή για την αναλογία, καθώς η τυπική απόκλιση δεν έχει την ίδια αποτελεσματικότητα όταν υπάρχουν αυτά τα ζητήματα.
• Ποσοστό απόδοσης χωρίς κίνδυνο - Χρησιμοποιείται για να εκτιμηθεί εάν κάποιος αποζημιώνεται σωστά για τον πρόσθετο κίνδυνο που βαρύνει το επικίνδυνο περιουσιακό στοιχείο. Παραδοσιακά, το ποσοστό απόδοσης χωρίς οικονομική ζημία είναι οι κρατικοί τίτλοι με τη μικρότερη διάρκεια (π.χ. US Treasury Bill). Ενώ μια τέτοια παραλλαγή ασφάλειας έχει το μικρότερο ποσοστό μεταβλητότητας, μπορεί να υποστηριχθεί ότι τέτοιοι τίτλοι πρέπει να ταιριάζουν με άλλους τίτλους ισοδύναμης διάρκειας.
• Τυπική απόκλιση - Είναι μια ποσότητα που εκφράζει πόσες μονάδες από ένα δεδομένο σύνολο μεταβλητών διαφέρουν από τον μέσο όρο της ομάδας. Μόλις υπολογιστεί αυτή η υπερβολική απόδοση έναντι της απόδοσης χωρίς κίνδυνο, πρέπει να διαιρεθεί με την τυπική απόκλιση του μελλοντικού κινδύνου. Όσο μεγαλύτερος είναι ο αριθμός, ελκυστική η επένδυση θα εμφανιστεί από την άποψη κινδύνου / απόδοσης. Ωστόσο, εκτός εάν η τυπική απόκλιση είναι ουσιαστικά μεγάλη, το στοιχείο μόχλευσης ενδέχεται να μην επηρεάσει την αναλογία. Τόσο ο αριθμητής (επιστροφή) όσο και ο παρονομαστής (τυπική απόκλιση) θα μπορούσαν να διπλασιαστούν χωρίς προβλήματα.

Παράδειγμα

Ο πελάτης «Α» διατηρεί επί του παρόντος 450.000 $ επενδυμένα σε ένα χαρτοφυλάκιο με αναμενόμενη απόδοση 12% και αστάθεια 10%. Το αποδοτικό χαρτοφυλάκιο έχει αναμενόμενη απόδοση 17% και αστάθεια 12%. Το επιτόκιο χωρίς κίνδυνο είναι 5%. Τι είναι η αναλογία Sharpe;

Τύπος Sharpe Ratio = (Αναμενόμενη απόδοση - Ποσοστό απόδοσης χωρίς κίνδυνο) / Τυπική απόκλιση (Μεταβλητότητα)

Αναλογία Sharpe = (0,12-0,05) / 0,10 = 70% ή 0,7x

Υπολογισμός αναλογίας Sharpe στο Excel

Τώρα που γνωρίζουμε πώς λειτουργεί ο τύπος, ας υπολογίσουμε το Sharpe Ratio στο excel.

Βήμα 1 - Λάβετε τις επιστροφές σε μορφή πίνακα

Το πρώτο βήμα περιλαμβάνει τη διευθέτηση των αποδόσεων του χαρτοφυλακίου του αμοιβαίου κεφαλαίου που θέλετε να αναλύσετε. Η χρονική περίοδος μπορεί να είναι μηνιαία, τριμηνιαία ή ετήσια. Ο παρακάτω πίνακας παρέχει ετήσιες αποδόσεις ενός αμοιβαίου κεφαλαίου.

Βήμα 2 - Λάβετε λεπτομέρειες επιστροφής χωρίς κίνδυνο στον πίνακα

Στον παρακάτω πίνακα, έχω υποθέσει ότι η απόδοση χωρίς κίνδυνο είναι 3,0% καθ 'όλη τη διάρκεια των 15 ετών. Ωστόσο, το ποσοστό χωρίς κίνδυνο μπορεί να αλλάζει κάθε χρόνο και πρέπει να βάλετε αυτόν τον αριθμό εδώ.

Βήμα 3 - Βρείτε υπερβολική απόδοση

Το τρίτο βήμα για τον υπολογισμό της αναλογίας Sharpe στο excel είναι να βρείτε τις υπερβολικές αποδόσεις του χαρτοφυλακίου. Στην περίπτωσή μας, η υπερβολική απόδοση είναι οι ετήσιες αποδόσεις - απόδοση χωρίς κίνδυνο.

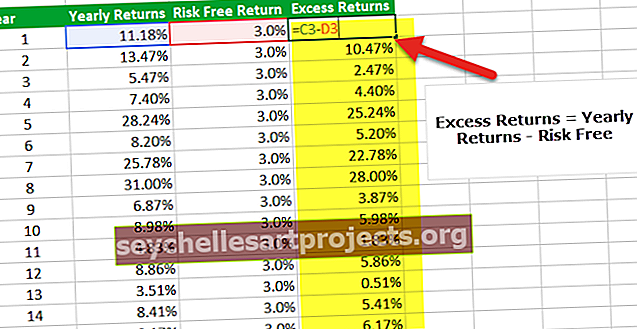
Βήμα 4 - Βρείτε τον μέσο όρο των ετήσιων επιστροφών.

Το τέταρτο βήμα για τον υπολογισμό του λόγου Sharpe στο excel είναι να βρείτε τον μέσο όρο των ετήσιων αποδόσεων. Μπορείτε να χρησιμοποιήσετε τον τύπο excel AVERAGE για να βρείτε τον μέσο όρο του χαρτοφυλακίου. Στο παράδειγμά μας, έχουμε μέση απόδοση 12,09%.

Βήμα 5 - Βρείτε μια τυπική απόκλιση των υπερβολικών αποδόσεων

Για να βρείτε την τυπική απόκλιση των υπερβολικών αποδόσεων, μπορείτε να χρησιμοποιήσετε τον τύπο excel STDEV όπως δίνεται παρακάτω.

Βήμα 6 - Υπολογισμός αναλογίας Sharpe

Το τελευταίο βήμα για τον υπολογισμό του λόγου Sharpe στο excel είναι να διαιρέσετε τις μέσες αποδόσεις με τυπική απόκλιση. Παίρνουμε την αναλογία = 12,09% / 8,8% = 1,37x

Παίρνουμε την αναλογία = 12,09% / 8,8% = 1,37x

Πλεονεκτήματα της χρήσης του λόγου Sharpe

# 1 - Το Sharpe Ratio βοηθά στη σύγκριση και την αντίθεση νέων προσθηκών

Χρησιμοποιείται για να συγκρίνει τη διακύμανση των συνολικών δυνατοτήτων απόδοσης χαρτοφυλακίου κάθε φορά που προστίθεται ένα νέο περιουσιακό στοιχείο ή μια κατηγορία περιουσιακών στοιχείων.

• Για παράδειγμα, ένας διαχειριστής χαρτοφυλακίου εξετάζει την προσθήκη μιας κατανομής αμοιβαίων κεφαλαίων στο υπάρχον επενδυτικό χαρτοφυλάκιο 80/20 με μετοχές με δείκτη Sharpe 0,81.
• Εάν η κατανομή του νέου χαρτοφυλακίου είναι 40/40/20 μετοχές, ομόλογα και κατανομή κεφαλαίων χρέους, ο λόγος Sharpe αυξάνεται σε 0,92.

Αυτό είναι μια ένδειξη ότι παρόλο που η επένδυση σε αμοιβαία κεφάλαια εμπορευμάτων είναι ασταθής ως αυτόνομη έκθεση, σε αυτήν την περίπτωση, στην πραγματικότητα οδηγεί σε βελτίωση του χαρακτηριστικού απόδοσης κινδύνου του συνδυασμένου χαρτοφυλακίου και συνεπώς προσθέτει ένα όφελος από διαφοροποίηση σε ένα άλλο περιουσιακό στοιχείο τάξη στο υπάρχον χαρτοφυλάκιο. Πρέπει να υπάρχει συμμετοχή προσεκτικής ανάλυσης ότι η κατανομή των κεφαλαίων ενδέχεται να χρειαστεί να αλλάξει σε μεταγενέστερο στάδιο, εάν έχει αρνητικές επιπτώσεις στην υγεία του χαρτοφυλακίου. Εάν η προσθήκη της νέας επένδυσης οδηγεί σε μείωση του λόγου, δεν θα πρέπει να συμπεριληφθεί στο χαρτοφυλάκιο.

# 2 - Το Sharpe Ratio βοηθά στη σύγκριση κινδύνου επιστροφής

Αυτή η αναλογία μπορεί επίσης να παρέχει καθοδήγηση σχετικά με το εάν οι υπερβολικές αποδόσεις ενός χαρτοφυλακίου οφείλονται σε προσεκτική λήψη επενδυτικών αποφάσεων ή σε αποτέλεσμα αδικαιολόγητων κινδύνων. Παρόλο που ένα μεμονωμένο αμοιβαίο κεφάλαιο ή χαρτοφυλάκιο μπορεί να απολαμβάνει μεγαλύτερες αποδόσεις από τους ομολόγους του, είναι λογική επένδυση μόνο εάν αυτές οι υψηλότερες αποδόσεις δεν συνοδεύονται από αδικαιολόγητους κινδύνους. Όσο μεγαλύτερη είναι η αναλογία Sharpe ενός χαρτοφυλακίου, τόσο καλύτερη είναι η απόδοσή του να συνυπολογίζει τη συνιστώσα κινδύνου. Ένας αρνητικός λόγος Sharpe δείχνει ότι το λιγότερο επικίνδυνο περιουσιακό στοιχείο θα έχει καλύτερη απόδοση από την ασφάλεια που αναλύεται.

Ας πάρουμε ένα παράδειγμα της σύγκρισης κινδύνου-απόδοσης.

Ας υποθέσουμε ότι το χαρτοφυλάκιο Α είχε ή αναμένεται να έχει ποσοστό απόδοσης 12% με τυπική απόκλιση 0,15. Υποθέτοντας μια απόδοση αναφοράς περίπου 1,5%, το ποσοστό απόδοσης (R) θα ήταν 0,12, το Rf θα είναι 0,015 και το 's' θα ήταν 0,15. Η αναλογία θα διαβαστεί ως (0,12 - 0,015) / 0,15 που υπολογίζεται σε 0,70. Ωστόσο, αυτός ο αριθμός θα έχει νόημα όταν συγκρίνεται με άλλο χαρτοφυλάκιο.

Εάν το χαρτοφυλάκιο «Β» εμφανίζει μεγαλύτερη μεταβλητότητα από το χαρτοφυλάκιο «Α» αλλά έχει την ίδια απόδοση, θα έχει μεγαλύτερη τυπική απόκλιση με τον ίδιο ρυθμό απόδοσης από το χαρτοφυλάκιο. Υποθέτοντας ότι η τυπική απόκλιση για το Χαρτοφυλάκιο Β είναι 0,20, η εξίσωση θα διαβαστεί ως (0,12 - 0,015) / 0,15. Ο λόγος Sharpe για αυτό το χαρτοφυλάκιο θα είναι 0,53 που είναι χαμηλότερος σε σύγκριση με το χαρτοφυλάκιο «A». Αυτό μπορεί να μην είναι εκπληκτικό αποτέλεσμα, λαμβάνοντας υπόψη το γεγονός ότι και οι δύο επενδύσεις είχαν την ίδια απόδοση, αλλά το «Β» είχε μεγαλύτερο κίνδυνο. Προφανώς, αυτός που έχει μικρότερο κίνδυνο να προσφέρει την ίδια απόδοση θα είναι μια προτιμώμενη επιλογή.

Κριτικές αναλογίες Sharpe

Ο λόγος Sharpe χρησιμοποιεί την τυπική απόκλιση των αποδόσεων στον παρονομαστή ως εναλλακτική λύση στους συνολικούς κινδύνους χαρτοφυλακίου, με την υπόθεση ότι οι αποδόσεις κατανέμονται ομοιόμορφα. Οι προηγούμενες δοκιμές έδειξαν ότι οι αποδόσεις από ορισμένα χρηματοοικονομικά περιουσιακά στοιχεία ενδέχεται να αποκλίνουν από την κανονική κατανομή, με αποτέλεσμα οι σχετικές ερμηνείες του λόγου Sharpe να είναι παραπλανητικές.

Αυτή η αναλογία μπορεί να βελτιωθεί από διάφορους διαχειριστές αμοιβαίων κεφαλαίων που προσπαθούν να ενισχύσουν την φαινομενικά προσαρμοσμένη απόδοση τους, η οποία μπορεί να εκτελεστεί ως εξής:

1. Αύξηση της χρονικής διάρκειας προς μέτρηση : Αυτό θα έχει ως αποτέλεσμα μικρότερη πιθανότητα μεταβλητότητας. Για παράδειγμα, η ετήσια τυπική απόκλιση των ημερήσιων αποδόσεων είναι γενικά υψηλότερη από την εβδομαδιαία απόδοση, η οποία με τη σειρά της είναι υψηλότερη από αυτήν των μηνιαίων αποδόσεων. Όσο μεγαλύτερη είναι η διάρκεια του χρόνου, τόσο πιο ξεκάθαρη εικόνα πρέπει να αποκλείσει τυχόν εφάπαξ παράγοντες που μπορούν να επηρεάσουν τη συνολική απόδοση.
2. Σύνθεση των μηνιαίων αποδόσεων αλλά υπολογισμός της τυπικής απόκλισης, εξαιρουμένης της πρόσφατα υπολογισμένης σύνθετης μηνιαίας απόδοσης
3. Γράφοντας αποφάσεις πώλησης και αγοράς ενός χαρτοφυλακίου εκτός χρημάτων: Μια τέτοια στρατηγική μπορεί δυνητικά να αυξήσει τις αποδόσεις συλλέγοντας το ασφάλιστρο επιλογών χωρίς να πληρώσει για αρκετά χρόνια. Οι στρατηγικές που συνεπάγονται αμφισβήτηση του προεπιλεγμένου κινδύνου, του κινδύνου ρευστότητας ή άλλων μορφών κινδύνων ευρείας εξάπλωσης έχουν την ίδια ικανότητα να αναφέρουν μια ανοδική μεροληπτική αναλογία Sharpe.
4. Ομαλοποίηση των αποδόσεων: Η χρήση ορισμένων παραγώγων δομών, η μη κανονική σήμανση στην αγορά λιγότερων ρευστών περιουσιακών στοιχείων ή η χρήση ορισμένων μοντέλων τιμολόγησης που υποτιμούν τα μηνιαία κέρδη ή ζημίες, μπορεί να μειώσει την αναμενόμενη αστάθεια.
5. Εξάλειψη ακραίων αποδόσεων: Οι υπερβολικά υψηλές ή πολύ χαμηλές αποδόσεις μπορούν να αυξήσουν την αναφερόμενη τυπική απόκλιση οποιουδήποτε χαρτοφυλακίου, καθώς είναι η απόσταση από το μέσο όρο. Σε μια τέτοια περίπτωση, ένας διαχειριστής κεφαλαίων μπορεί να επιλέξει να εξαλείψει τις ακραίες τελικές (καλύτερες και χειρότερες) μηνιαίες αποδόσεις κάθε χρόνο για να μειώσει την τυπική απόκλιση και να επηρεάσει τα αποτελέσματα, καθώς μια τέτοια εφάπαξ κατάσταση μπορεί να επηρεάσει τον συνολικό μέσο όρο.

Λόγος Ex-Ante και Ex-Post Sharpe

Ο λόγος Sharpe έχει αναθεωρηθεί πολλές φορές, αλλά δύο γενικές μορφές που έχουν χρησιμοποιηθεί είναι εκ των προτέρων (πρόβλεψη μελλοντικής απόδοσης και διακύμανσης) και εκ των υστέρων (ανάλυση προηγούμενης απόδοσης επιστροφής).

• Οι προβλέψεις αναλογίας εκ των προτέρων Sharpe είναι απλές για την εκτίμηση των προτύπων μετά από παρατηρήσεις της προηγούμενης απόδοσης παρόμοιων επενδυτικών δραστηριοτήτων.
• Το Ex-post Sharpe Ratio μετρά πόσο υψηλή ήταν η απόδοση, σε σύγκριση με το πόσο ποικίλες ήταν αυτές οι αποδόσεις σε μια δεδομένη χρονική περίοδο. Πιο συγκεκριμένα, είναι ο λόγος των διαφορικών αποδόσεων (η διαφορά μεταξύ των αποδόσεων στην επένδυση και μιας επένδυσης αναφοράς) έναντι της ιστορικής μεταβλητότητας (τυπική απόκλιση) αυτών των αποδόσεων.

συμπέρασμα

Η αναλογία Sharpe είναι ένα τυπικό μέτρο της απόδοσης του χαρτοφυλακίου. Λόγω της απλότητας και της ευκολίας της ερμηνείας, είναι ένα από τα πιο δημοφιλή ευρετήρια. Δυστυχώς, οι περισσότεροι χρήστες ξεχνούν τις παραδοχές που οδηγούν σε ακατάλληλο αποτέλεσμα. Θα πρέπει να εξετάσετε το ενδεχόμενο να ελέγξετε την κατανομή των αποδόσεων ή την επικύρωση των αποτελεσμάτων με ισοδύναμα μέτρα απόδοσης πριν λάβετε μια απόφαση στην αγορά.