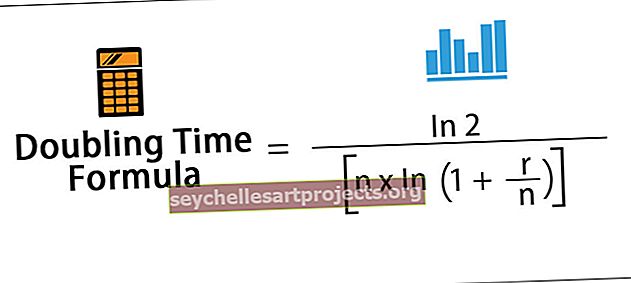Time Value of Money (TVM) - Ορισμός, έννοιες και παραδείγματα
Ορισμός χρόνου αξίας χρημάτων
Time Value of Money (TVM) σημαίνει ότι τα χρήματα που λαμβάνονται σήμερα είναι υψηλότερης αξίας από τα χρήματα που θα λαμβάνονται στο μέλλον, καθώς τα χρήματα που λαμβάνονται τώρα μπορούν να επενδυθούν και μπορεί να δημιουργήσει ταμειακές ροές στην επιχείρηση στο μέλλον με τρόπο ενδιαφέροντος ή από επενδύσεις εκτίμηση στο μέλλον και από την επανεπένδυση.
Η αξία χρόνου χρήματος αναφέρεται επίσης ως παρούσα έκπτωση. Τα χρήματα που κατατίθενται σε έναν τραπεζικό λογαριασμό ταμιευτηρίου κερδίζουν ένα συγκεκριμένο επιτόκιο για να αντισταθμίσουν τη διατήρηση των χρημάτων από αυτά στην τρέχουσα χρονική στιγμή. Επομένως, εάν ένας κάτοχος τράπεζας καταθέσει 100 $ στον λογαριασμό, η προσδοκία θα είναι να λάβει περισσότερα από 100 $ μετά από ένα έτος.
Εξήγηση
Time Value of Money είναι μια έννοια που αναγνωρίζει τη σχετική αξία των μελλοντικών ταμειακών ροών που προκύπτουν ως αποτέλεσμα οικονομικών αποφάσεων λαμβάνοντας υπόψη το κόστος ευκαιρίας των κεφαλαίων. Δεδομένου ότι το χρήμα τείνει να χάνει αξία με την πάροδο του χρόνου, υπάρχει πληθωρισμός που μειώνει την αγοραστική δύναμη του χρήματος. Ωστόσο, το κόστος λήψης χρημάτων στο μέλλον και όχι τώρα θα είναι μεγαλύτερο από απλώς την απώλεια στην πραγματική του αξία λόγω του πληθωρισμού. Το κόστος ευκαιρίας του να μην έχετε τα χρήματα τώρα περιλαμβάνει επίσης την απώλεια πρόσθετου εισοδήματος που θα μπορούσε να αποκτηθεί με την κατοχή μετρητών νωρίτερα.
Επιπλέον, η λήψη χρημάτων στο μέλλον και όχι τώρα μπορεί να συνεπάγεται κάποιο κίνδυνο και αβεβαιότητα σχετικά με την ανάκτησή τους. Για αυτούς τους λόγους, οι μελλοντικές ταμειακές ροές αξίζουν λιγότερο από τις τρέχουσες ταμειακές ροές.
Top 6 Time Value of Money Concepts
# 1 - Μελλοντική αξία ενός ποσού
Το πρώτο στην έννοια χρονικής αξίας του χρήματος που συζητάμε είναι να υπολογίσουμε τη μελλοντική αξία ενός μεμονωμένου ποσού.
Ας υποθέσουμε ότι κάποιος επενδύει 1.000 $ για 3 χρόνια σε λογαριασμό ταμιευτηρίου που πληρώνει 10% τόκους ετησίως. Εάν κάποιος επιτρέπει την επανεπένδυση των εσόδων από τόκους, η επένδυση θα αυξηθεί ως εξής:
Μελλοντική αξία στο τέλος του πρώτου έτους

- Διευθυντής στις αρχές του έτους 1.000 $
- Τόκοι για το έτος ($ 1.000 * 0,10 $) 100 $
- Κύριος στο τέλος 1.100 $
Μελλοντική αξία στο τέλος του δεύτερου έτους

- Διευθυντής στις αρχές του έτους 1.100 $
- Τόκοι για το έτος (1,100 $ 0,10 $) 110 $
- Κύριος στο τέλος 1.210 $
Η διαδικασία επένδυσης χρημάτων και επανεπένδυσης των κερδών που κερδίζονται ονομάζεται Compounding. Η μελλοντική αξία ή η σύνθετη αξία μιας επένδυσης μετά το έτος "n" όταν το επιτόκιο είναι "r" % είναι:
FV = PV (1 + r) n
Σύμφωνα με την παραπάνω εξίσωση, το (1 + r) n ονομάζεται μελλοντικός συντελεστής τιμής. Υπάρχουν προκαθορισμένοι πίνακες που καθορίζουν το επιτόκιο και την αξία του μετά τον αριθμό «n» ετών. Μπορεί επίσης να χρησιμοποιηθεί με τη βοήθεια μιας αριθμομηχανής ή ενός υπολογιστικού φύλλου excel. Το παρακάτω στιγμιότυπο είναι μια παρουσία του τρόπου υπολογισμού του επιτοκίου για διαφορετικά επιτόκια και σε διαφορετικά χρονικά διαστήματα.
Ως εκ τούτου, με την παραπάνω περίπτωση, το FV των $ 1.000 μπορεί να χρησιμοποιηθεί ως:
FV = 1000 (1.210) = 1210 $
# 2 - Χρόνος αξίας χρημάτων: Διπλή περίοδος
Η πρώτη σημαντική πτυχή της έννοιας χρονικής αξίας χρήματος (TVM) είναι η περίοδος διπλασιασμού.
Οι επενδυτές γενικά επιθυμούν να γνωρίζουν πότε η επένδυσή τους μπορεί να διπλασιαστεί με ένα δεδομένο ενδιαφέρον. Αν και είναι λίγο αργό, ένας καθιερωμένος κανόνας είναι ο «Κανόνας του 72» που δηλώνει ότι η περίοδος διπλασιασμού μπορεί να επιτευχθεί διαιρώντας το 72 με το επιτόκιο.
Για παράδειγμα, εάν ο τόκος είναι 8%, η περίοδος διπλασιασμού είναι 9 έτη [72/8 = 9 έτη].

Ένας ελαφρώς πιο υπολογιστικός κανόνας είναι ο «Κανόνας του 69» που δηλώνει την περίοδο διπλασιασμού ως 0,35 + 69 / Τόκος
# 3 - Τρέχουσα αξία ενός ενιαίου ποσού
Το τρίτο σημαντικό σημείο στην έννοια της χρονικής αξίας του χρήματος (TVM) είναι να βρεθεί η παρούσα αξία ενός μόνο ποσού.
Αυτό το σενάριο δηλώνει την παρούσα αξία ενός χρηματικού ποσού που αναμένεται να ληφθεί μετά από μια δεδομένη χρονική περίοδο. Η διαδικασία έκπτωσης που χρησιμοποιείται για τον υπολογισμό της παρούσας αξίας είναι απλά το αντίστροφο της σύνθεσης. Ο Φ / Β τύπος μπορεί να ληφθεί εύκολα χρησιμοποιώντας τον παρακάτω τύπο:
PV = FV n [1 / (1 + r) n]
Για παράδειγμα, εάν ένας πελάτης αναμένεται να λάβει 1.000 $ μετά από 3 χρόνια @ 8% ROI, η αξία του την παρούσα στιγμή μπορεί να υπολογιστεί ως:

PV = 1000 [1 / 1,08] 3
PV = 1000 * 0,779 = 794 $
# 4 - Μελλοντική αξία ενός προσόδου
Η τέταρτη σημαντική ιδέα της έννοιας της χρονικής αξίας του χρήματος (TVM) είναι ο υπολογισμός της μελλοντικής αξίας μιας προσόδου.
Μια πρόσοδος είναι μια ροή σταθερών ταμειακών ροών (εισπράξεις ή πληρωμές) που συμβαίνουν σε κανονικά χρονικά διαστήματα. Οι πληρωμές ασφαλίστρων ενός ασφαλιστηρίου συμβολαίου ζωής, για παράδειγμα, είναι μια πρόσοδος. Όταν οι ταμειακές ροές συμβαίνουν στο τέλος κάθε περιόδου, η πρόσοδος ονομάζεται Συνηθισμένη πρόσοδος ή αναβαλλόμενη πρόσοδος. Όταν αυτή η ροή συμβαίνει στην αρχή κάθε περιόδου, ονομάζεται Προθεσμία λήξης Ο τύπος για μια οφειλόμενη πρόσοδος είναι απλώς (1 + r) φορές ο τύπος για την αντίστοιχη συνήθης πρόσοδος. Η εστίασή μας θα είναι περισσότερο στην αναβαλλόμενη πρόσοδος.
Ας πάρουμε ένα παράδειγμα με το οποίο κάποιος καταθέτει 1.000 $ ετησίως σε μια τράπεζα για 5 χρόνια και η κατάθεση κερδίζει σύνθετους τόκους σε 10% ROI, την αξία της σειράς καταθέσεων στο τέλος των 5 ετών:

Μελλοντική τιμή = 1.000 $ (1 + 1.10) 4 + 1.000 $ (1 + 1.10) 3 + 1.000 $ (1 + 1.10) 2 + 1.000 $ (1.10) + 1.000 $ = 6.105 $
Σε γενικές γραμμές, η μελλοντική τιμή της προσόδου δίνεται από τον ακόλουθο τύπο:
- FVA n = A [(1 + r) n - 1] / r
- Το FVA n είναι το FV του προσόδου που έχει διάρκεια περιόδων «n», το «A» είναι η σταθερή περιοδική ροή και το «r» είναι το ROI ανά περίοδο. Ο όρος [(1 + r) n - 1] / r αναφέρεται ως ο μελλοντικός συντελεστής επιτοκίου αξίας για μια πρόσοδο.
# 5 - Τρέχουσα αξία προσόδων
Η πέμπτη σημαντική έννοια της έννοιας χρονικής αξίας του χρήματος είναι ο υπολογισμός της παρούσας αξίας ενός προσόδων.
Αυτή η ιδέα είναι μια αντιστροφή της μελλοντικής τιμής προσόδου αντί για FV, η εστίαση θα είναι στο PV. Ας υποθέσουμε ότι κάποιος αναμένει να λάβει 1.000 $ ετησίως για 3 χρόνια, με κάθε απόδειξη να πραγματοποιείται στο τέλος του έτους, το φωτοβολταϊκό αυτής της ροής παροχών με προεξοφλητικό επιτόκιο 10% θα υπολογιζόταν ως εξής:

1.000 $ [1 / 1.10] + 1.000 [1 / 1.10] 2 + 1.000 [1 / 1.10] 3 = 2.486,80 $
Σε γενικές γραμμές, η παρούσα αξία ενός προσόμου μπορεί να εκφραστεί ως εξής:
- A = [{1 - (1/1 + r) n} / r]
# 6 - Τρέχουσα αξία της διαιώνιας
Η έκτη έννοια στη χρονική αξία του χρήματος (TVM) είναι να βρεθεί η παρούσα αξία μιας διαιώνιας.
Η διαιώνιση είναι μια πρόσοδος αορίστου χρόνου. Για παράδειγμα, η βρετανική κυβέρνηση έχει εκδώσει ομόλογα που ονομάζονται «κονσόλες» τα οποία καταβάλλουν ετήσιους τόκους καθ 'όλη τη διάρκεια της ύπαρξής της. Αν και η συνολική ονομαστική αξία της διαιώνιας είναι απεριόριστη και απροσδιόριστη, η παρούσα αξία του δεν είναι. Σύμφωνα με την αρχή Time Value of Money (TVM), η παρούσα αξία της διαχρονικής αξίας είναι το άθροισμα της προεξοφλημένης αξίας κάθε περιοδικής πληρωμής του διαρκείας. Ο τύπος για τον υπολογισμό της παρούσας αξίας της διαχρονικότητας είναι:
Διορθώθηκε η περιοδική πληρωμή / ROI ή το προεξοφλητικό επιτόκιο ανά περίοδο σύνθεσης

Για παράδειγμα, για τον υπολογισμό της φωτοβολταϊκής ισχύος την 1η Ιανουαρίου 2015, η διαχρονική καταβολή 1.000 $ στο τέλος κάθε μήνα ξεκινώντας από τον Ιανουάριο του 2015 με μηνιαίο προεξοφλητικό επιτόκιο 0.
- PV = 1.000 $ / 0,8% = 125.000 $
Αυξανόμενη διαιώνια
Αυτό είναι ένα σενάριο στο οποίο η διαιώνιση θα συνεχίσει να αλλάζει όπως οι πληρωμές ενοικίου. Για παράδειγμα, ένα συγκρότημα γραφείων αναμένεται να αποφέρει καθαρή ενοικίαση ύψους 3 εκατομμυρίων δολαρίων για το επόμενο έτος, το οποίο αναμένεται να αυξάνεται κατά 5% κάθε χρόνο. Εάν υποθέσουμε ότι η αύξηση θα συνεχιστεί επ 'αόριστον, το σύστημα ενοικίασης θα χαρακτηριστεί ως αυξανόμενη διαρκής. Εάν το προεξοφλητικό επιτόκιο είναι 10%, το PV της ροής ενοικίασης θα είναι:

Σε έναν αλγεβρικό τύπο, μπορεί να εμφανιστεί ως εξής,
- PV = C / rg, όπου το "C" είναι το ενοίκιο που θα ληφθεί κατά τη διάρκεια του έτους, το "r" είναι το ROI και το "g" είναι ο ρυθμός ανάπτυξης.
Χρόνος αξίας χρημάτων - Ενδοετής Συγκέντρωση & Εκπτώσεις
Σε αυτήν την περίπτωση, εξετάζουμε την περίπτωση όπου η ένωση γίνεται σε συχνή βάση. Υποθέτοντας ότι ένας πελάτης καταθέτει 1.000 $ σε μια εταιρεία χρηματοδότησης που πληρώνει 12% τόκους σε εξαμηνιαία βάση που δείχνει ότι το ποσό των τόκων καταβάλλεται κάθε 6 μήνες. Το ποσό της κατάθεσης θα αυξηθεί ως εξής:
- Πρώτοι έξι μήνες: Διευθυντής στην αρχή = 1.000 $
- Τόκος για 6 μήνες = 60 $ (1.000 $ * 12%) / 2
- Κύριος στο τέλος = 1.000 $ + 60 $ = 1.060 $
Επόμενοι έξι μήνες: Διευθυντής στην αρχή = 1.060 $
- Τόκος για 6 μήνες = 63,6 $ (1.060 $ * 12%) / 2
- Κύριος στο τέλος = 1.060 $ + 63,6 $ = 1,123,6 $
Πρέπει να σημειωθεί ότι εάν η σύνθεση γίνεται ετησίως, ο κύριος υπολογιστής στο τέλος ενός έτους θα είναι 1.000 $ 1,12 = 1.120 $. Η διαφορά 3,6 $ (μεταξύ 1,123,6 $ για την εξαμηνιαία ένωση και 1,120 $ για την ετήσια ένωση) αντιπροσωπεύει τους τόκους για το δεύτερο εξάμηνο.
Παραδείγματα αξίας χρόνου χρήματος

Παράδειγμα # 1 - Μοντέλο έκπτωσης μερισμάτων
Αυτό είναι ένα πραγματικό παράδειγμα χρόνου αξίας χρήματος για τη χρήση του σε αποτιμήσεις χρησιμοποιώντας το μοντέλο έκπτωσης μερισμάτων.
Το μοντέλο έκπτωσης μερισμάτων τιμολογεί μια μετοχή προσθέτοντας τις μελλοντικές ταμειακές ροές προεξοφλημένες από τον απαιτούμενο ρυθμό απόδοσης που ένας επενδυτής απαιτεί για τον κίνδυνο κατοχής της μετοχής.
Εδώ το CF = Μερίσματα.
Ωστόσο, αυτή η κατάσταση είναι λίγο θεωρητική, καθώς οι επενδυτές συνήθως επενδύουν σε μετοχές τόσο για μερίσματα όσο και για ανατίμηση κεφαλαίου. Η ανατίμηση κεφαλαίου είναι όταν πουλάτε το απόθεμα σε υψηλότερη τιμή, τότε αγοράζετε. Σε μια τέτοια περίπτωση, υπάρχουν δύο ταμειακές ροές -
- Μελλοντικές πληρωμές μερισμάτων
- Μελλοντική τιμή πώλησης
Εσωτερική αξία = Άθροισμα της παρούσας αξίας των μερισμάτων + παρούσα αξία της τιμής πώλησης μετοχών
Αυτή η τιμή DDM είναι η εγγενής αξία του αποθέματος.
Ας πάρουμε ένα παράδειγμα μοντέλου DDM με έκπτωση μερισμάτων εδώ.
Ας υποθέσουμε ότι σκέφτεστε να αγοράσετε ένα απόθεμα που θα πληρώσει μερίσματα 20 $ (Div 1) τον επόμενο χρόνο και 21,6 $ (Div 2) τον επόμενο χρόνο. Αφού λάβετε το δεύτερο μέρισμα, σκοπεύετε να πουλήσετε το απόθεμα για 333,3 $. Ποια είναι η εγγενής αξία αυτού του αποθέματος εάν η απαιτούμενη απόδοση σας είναι 15%;
Αυτό το πρόβλημα μπορεί να επιλυθεί σε 3 βήματα -
Βήμα 1 - Βρείτε την παρούσα αξία των μερισμάτων για το έτος 1 και το έτος 2.
- PV (έτος 1) = 20 $ / ((1,15) ^ 1)
- PV (έτος 2) = 20 $ / ((1,15) ^ 2)
- Σε αυτό το παράδειγμα, βγαίνουν 17,4 $ και 16,3 $ αντίστοιχα για το μέρισμα 1ου και 2ου έτους.
Βήμα 2 - Βρείτε την παρούσα αξία της μελλοντικής τιμής πώλησης μετά από δύο χρόνια.
- PV (Τιμή πώλησης) = 333,3 $ / (1,15 ^ 2)
Βήμα 3 - Προσθέστε την παρούσα αξία μερισμάτων και την παρούσα αξία της τιμής πώλησης
- 17,4 $ + 16,3 $ + 252,0 $ = 285,8 $
Παράδειγμα # 2 - Υπολογιστής EMI δανείου
Ένα δάνειο εκδίδεται στις αρχές του έτους 1. Το κεφάλαιο είναι 15.000.000 $, το επιτόκιο είναι 10% και ο όρος είναι 60 μήνες. Οι αποπληρωμές πρέπει να γίνονται στο τέλος κάθε μήνα. Το δάνειο πρέπει να εξοφληθεί πλήρως μέχρι το τέλος της περιόδου.
- Κύριος - 15.000.000 $
- Επιτόκιο (μηνιαίο) - 1%
- Διάρκεια = 60 μήνες
Για να βρούμε την Ίση Μηνιαία Δόση ή EMI, μπορούμε να χρησιμοποιήσουμε τη συνάρτηση PMT στο Excel. Απαιτεί την αρχή, το ενδιαφέρον και τον όρο ως εισροές.

EMI = 33.367 $ ανά μήνα
Παράδειγμα # 3 - Εκτίμηση Alibaba
Ας δούμε πώς εφαρμόστηκε η έννοια Time Value of Money (TVM) για την αποτίμηση της Alibaba IPO. Για την αποτίμηση της Alibaba, είχα κάνει την ανάλυση των οικονομικών καταστάσεων και πρόβλεψα τις οικονομικές καταστάσεις και έπειτα υπολόγισα τη δωρεάν ταμειακή ροή στην εταιρεία. Μπορείτε να κατεβάσετε το Alibaba Financial Model εδώ
Παρακάτω παρουσιάζεται η Δωρεάν Ταμειακή Ροή στην Εταιρεία της Alibaba. Η ελεύθερη ταμειακή ροή χωρίζεται σε δύο μέρη - α) Ιστορικό FCFF και β) Πρόβλεψη FCFF
- Το Ιστορικό FCFF διατίθεται από την Κατάσταση Αποτελεσμάτων, τον Ισολογισμό και τις Ταμειακές Ροές της εταιρείας από τις Ετήσιες Εκθέσεις της
- Η πρόβλεψη FCFF υπολογίζεται μόνο μετά την πρόβλεψη των οικονομικών καταστάσεων (το ονομάζουμε ως προετοιμασία του χρηματοοικονομικού μοντέλου στο excel) Ο βασικός χρηματοοικονομικός μοντελισμός είναι ελαφρώς δύσκολος και δεν θα συζητήσω τις λεπτομέρειες και τους τύπους των χρηματοοικονομικών μοντέλων σε αυτό το άρθρο.
- Προκειμένου να βρούμε την αποτίμηση της Alibaba, πρέπει να βρούμε την παρούσα αξία όλων των μελλοντικών οικονομικών ετών (μέχρι τη διαρκή - Τελική αξία)
- Για μια πλήρη ανάλυση, μπορείτε να ανατρέξετε σε αυτήν τη λεπτομερή σημείωση - Μοντέλο αποτίμησης Alibaba
συμπέρασμα
Η έννοια Time Value of Money προσπαθεί να ενσωματώσει τις παραπάνω εκτιμήσεις σε χρηματοοικονομικές αποφάσεις διευκολύνοντας μια αντικειμενική αξιολόγηση των ταμειακών ροών από διαφορετικές χρονικές περιόδους μετατρέποντάς τις σε παρούσα αξία ή μελλοντικά ισοδύναμα αξίας. Αυτό θα προσπαθήσει μόνο να εξουδετερώσει την παρούσα και τη μελλοντική αξία του χρήματος και να καταλήξει σε ομαλές οικονομικές αποφάσεις.