Τύπος διάρκειας (Ορισμός, παραδείγματα Excel) | Υπολογίστε τη διάρκεια του ομολόγου
Τι είναι ο τύπος διάρκειας;
Ο τύπος για τη διάρκεια είναι ένα μέτρο της ευαισθησίας ενός ομολόγου σε μεταβολές στο επιτόκιο και υπολογίζεται διαιρώντας το συνολικό προϊόν της προεξοφλημένης μελλοντικής ταμειακής εισροής του ομολόγου και έναν αντίστοιχο αριθμό ετών με ένα άθροισμα της προεξοφλημένης μελλοντικής εισροής μετρητών. Η εισροή μετρητών περιλαμβάνει βασικά την πληρωμή κουπονιών και τη λήξη στο τέλος. Είναι επίσης γνωστό ως διάρκεια Macaulay.
Μαθηματικά, η εξίσωση για τη διάρκεια παρουσιάζεται όπως παρακάτω,

που,
- C = Πληρωμή κουπονιού ανά περίοδο
- M = Ονομαστική ή ονομαστική τιμή
- r = Πραγματικό περιοδικό επιτόκιο
- n = Αριθμός περιόδων έως τη λήξη
Περαιτέρω, ο παρονομαστής που είναι το άθροισμα της προεξοφλημένης ταμειακής εισροής του ομολόγου ισοδυναμεί με την παρούσα αξία ή τιμή του ομολόγου. Επομένως, ο τύπος για τη διάρκεια μπορεί να απλοποιηθεί περαιτέρω όπως παρακάτω,

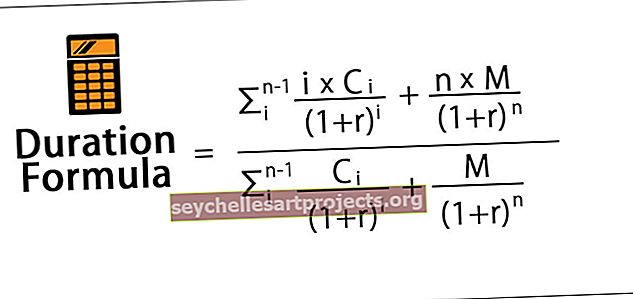
Επεξήγηση του τύπου Διάρκεια
Η εξίσωση για τη διάρκεια μπορεί να υπολογιστεί χρησιμοποιώντας τα ακόλουθα βήματα:
Βήμα 1: Πρώτον, η ονομαστική ή ονομαστική αξία της έκδοσης ομολόγων υπολογίζεται και υποδηλώνεται από τον Μ.
Βήμα 2: Τώρα, η πληρωμή με κουπόνι του ομολόγου υπολογίζεται με βάση το πραγματικό περιοδικό επιτόκιο. Στη συνέχεια, καθορίζεται επίσης η συχνότητα πληρωμής του κουπονιού. Η πληρωμή του κουπονιού υποδηλώνεται με C και το πραγματικό περιοδικό επιτόκιο δηλώνεται με r.
Βήμα 3: Τώρα, ο συνολικός αριθμός περιόδων έως τη λήξη υπολογίζεται πολλαπλασιάζοντας τον αριθμό ετών έως τη λήξη και τη συχνότητα των πληρωμών κουπονιών σε ένα έτος. Ο αριθμός των περιόδων έως τη λήξη δηλώνεται με n. Επίσης, σημειώνεται ο χρόνος της περιοδικής πληρωμής που δηλώνεται με το i.
Βήμα 4: Τέλος, με βάση τις διαθέσιμες πληροφορίες η εξίσωση για τη διάρκεια μπορεί να εξαχθεί όπως παρακάτω,

Παραδείγματα τύπου διάρκειας (με πρότυπο Excel)
Ας δούμε μερικούς απλούς έως προχωρημένους τύπους διάρκειας για να τον κατανοήσουμε καλύτερα.
Μπορείτε να κατεβάσετε αυτό το Πρότυπο Formula Excel διάρκειας εδώ - Πρότυπο Duration Formula Excel
Τύπος διάρκειας Τύπος - Παράδειγμα # 1
Ας πάρουμε ένα παράδειγμα ομολόγου με ετήσιες πληρωμές κουπονιών. Ας υποθέσουμε ότι η εταιρεία XYZ Ltd έχει εκδώσει ομόλογο με ονομαστική αξία 100.000 $, με ετήσιο επιτόκιο κουπονιού 7% και λήξη σε 5 χρόνια. Το ισχύον επιτόκιο της αγοράς είναι 10% .
Δεδομένου, M = 100.000 $
- C = 7% * 100.000 $ = 7.000 $
- n = 5
- r = 10%
Ο παρονομαστής ή η τιμή του ομολόγου υπολογίζεται χρησιμοποιώντας τον τύπο ως,

- Τιμή ομολόγου = 84.281,19
Ο υπολογισμός του αριθμητή του τύπου Διάρκεια έχει ως εξής -

= (6,363,64 + 11,570,25 + 15,777,61 + 19,124,38 + 310,460,70)
= 363,296,50
Επομένως, ο υπολογισμός της διάρκειας του ομολόγου θα είναι όπως παρακάτω,

Διάρκεια = 363.296.50 / 84.281.19
- Διάρκεια = 4,31 έτη
Τύπος διάρκειας Τύπος - Παράδειγμα # 2
Ας πάρουμε ένα παράδειγμα ομολόγου με ετήσιες πληρωμές κουπονιών. Ας υποθέσουμε ότι η εταιρεία XYZ Ltd έχει εκδώσει ομόλογο ονομαστικής αξίας $ 100.000 και λήγει σε 4 χρόνια. Το ισχύον επιτόκιο της αγοράς είναι 10%. Υπολογίστε τη διάρκεια του ομολόγου για το ακόλουθο ετήσιο επιτόκιο κουπονιού: (α) 8% (β) 6% (γ) 4%
Δεδομένου, M = 100.000 $
- n = 4
- r = 10%
Υπολογισμός για ποσοστό κουπονιού 8%
Πληρωμή κουπονιού (C) = 8% * 100.000 $ = 8.000 $
Ο παρονομαστής ή η τιμή του ομολόγου υπολογίζεται χρησιμοποιώντας τον τύπο ως,

- Τιμή ομολόγου = 88.196,16
Ο υπολογισμός του αριθμητή του τύπου Διάρκεια θα έχει ως εξής -

= 311,732,8
Επομένως, ο υπολογισμός της διάρκειας του ομολόγου θα είναι όπως παρακάτω,

Διάρκεια = 311,732,81 / 88,196,16
- Διάρκεια = 3,53 έτη
Υπολογισμός ποσοστού κουπονιού 6%
Πληρωμή κουπονιού (C) = 6% * 100.000 $ = 6.000 $
Ο παρονομαστής ή η τιμή του ομολόγου υπολογίζεται χρησιμοποιώντας τον τύπο ως,

- Τιμή ομολόγου = 83.222,46
Ο υπολογισμός του αριθμητή του τύπου Διάρκεια θα έχει ως εξής -

= 302,100,95
Επομένως, ο υπολογισμός της διάρκειας του ομολόγου θα είναι όπως παρακάτω,

Διάρκεια = 302.100.95 / 83.222.46
- Διάρκεια = 63 έτη
Υπολογισμός για ποσοστό κουπονιού 4%
Πληρωμή κουπονιού = 4% * 100.000 $ = 4.000 $
Ο παρονομαστής ή η τιμή του ομολόγου υπολογίζεται χρησιμοποιώντας τον τύπο ως,

- Τιμή ομολόγου = 78.248.75
Ο υπολογισμός του αριθμητή του τύπου Διάρκεια θα έχει ως εξής -

= 292,469,09
Επομένως, ο υπολογισμός της διάρκειας του ομολόγου θα είναι όπως παρακάτω,

Τύπος διάρκειας = 292.469.09 / 78.248.75
- Διάρκεια = 3,74 έτη
Από το παράδειγμα, μπορεί να φανεί ότι η διάρκεια ενός ομολόγου αυξάνεται με τη μείωση του ποσοστού κουπονιού.
Συνάφεια και χρήση της φόρμουλας διάρκειας
Είναι σημαντικό να κατανοήσουμε την έννοια της διάρκειας καθώς χρησιμοποιείται από τους επενδυτές ομολόγων για να ελέγξει την ευαισθησία ενός ομολόγου σε αλλαγές στα επιτόκια. Η διάρκεια ενός ομολόγου δείχνει βασικά πόσο θα αλλάξει η αγοραία τιμή ενός ομολόγου λόγω της μεταβολής του επιτοκίου. Αξίζει να σημειωθεί ότι το επιτόκιο και η τιμή των ομολόγων κινούνται σε αντίθετες κατευθύνσεις και ως εκ τούτου η τιμή των ομολόγων αυξάνεται όταν το επιτόκιο πέφτει και αντιστρόφως.
Σε περίπτωση που οι επενδυτές ζητούν όφελος από την πτώση του επιτοκίου, οι επενδυτές σκοπεύουν να αγοράσουν ομόλογα μεγαλύτερης διάρκειας, κάτι που είναι δυνατό σε περίπτωση ομολόγων με χαμηλότερη πληρωμή κουπονιού και μεγάλη διάρκεια. Από την άλλη πλευρά, οι επενδυτές που θέλουν να αποφύγουν τη μεταβλητότητα του επιτοκίου, οι επενδυτές θα πρέπει να επενδύσουν σε ομόλογα που έχουν χαμηλότερη διάρκεια ή μικρή διάρκεια και υψηλότερη πληρωμή κουπονιού.