Μέσος τύπος πληθυσμού | Υπολογισμός μέσου πληθυσμού (παραδείγματα)
Τύπος για τον υπολογισμό του μέσου πληθυσμού
Ο μέσος όρος του πληθυσμού είναι ο μέσος όρος ή ο μέσος όρος όλων των τιμών στον δεδομένο πληθυσμό και υπολογίζεται με το άθροισμα όλων των τιμών στον πληθυσμό που υποδηλώνονται με το άθροισμα του Χ διαιρούμενο με τον αριθμό των τιμών στον πληθυσμό που δηλώνεται με Ν.
Αυτό επιτυγχάνεται συνοψίζοντας όλες τις παρατηρήσεις στην ομάδα και διαιρώντας το άθροισμα με τον αριθμό των παρατηρήσεων. Όταν το σύνολο των δεδομένων λαμβάνονται για τον υπολογισμό μιας στατιστικής παραμέτρου, το σύνολο των δεδομένων είναι ο πληθυσμός. Για παράδειγμα, οι αποδόσεις όλων των μετοχών που αναφέρονται στο χρηματιστήριο NASDAQ στον πληθυσμό αυτής της ομάδας. Για αυτό το παράδειγμα, ο μέσος πληθυσμός για την απόδοση όλων των μετοχών που αναφέρονται στο χρηματιστήριο NASDAQ θα είναι ο μέσος όρος της απόδοσης όλων των μετοχών που αναφέρονται στο εν λόγω χρηματιστήριο.
Για να υπολογίσουμε το μέσο όρο του πληθυσμού για μια ομάδα πρέπει πρώτα να μάθουμε το άθροισμα όλων των παρατηρούμενων τιμών. Έτσι, εάν ο συνολικός αριθμός των παρατηρούμενων τιμών συμβολίζεται με το Χ, τότε το άθροισμα όλων των παρατηρούμενων τιμών θα είναι ∑X. Και αφήστε τον αριθμό των παρατηρήσεων στον πληθυσμό να είναι Ν.
Ο τύπος παρουσιάζεται ως εξής,
µ = ∑X / N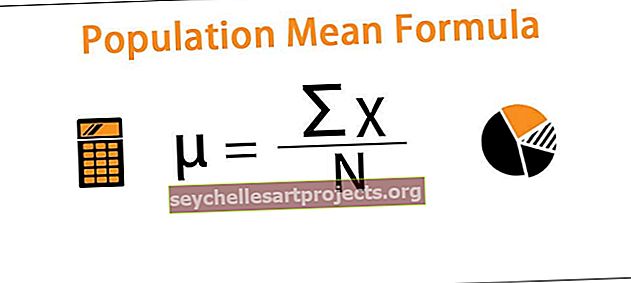
- μ = Μέσος πληθυσμός
Παραδείγματα
Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου για τον τύπο μέσου πληθυσμού Excel - Πρότυπο για τον μέσο όρο του πληθυσμού ExcelΠαράδειγμα # 1
Ας προσπαθήσουμε να αναλύσουμε την απόδοση μιας μετοχής XYZ τα τελευταία δώδεκα χρόνια. Και οι αποδόσεις για το απόθεμα τα τελευταία δώδεκα χρόνια είναι 12%, 25%, 16%, 14%, 40%, 15%, 13%, 17%, 23%, 13%, 17% και 19%. Για να υπολογίσουμε το μέσο όρο για ολόκληρο τον πληθυσμό, πρέπει πρώτα να ανακαλύψουμε το άθροισμα όλων των παρατηρούμενων τιμών. Έτσι, σε αυτό το παράδειγμα, το ∑X είναι 224% και ο αριθμός των τιμών που παρατηρήθηκαν για τον πληθυσμό είναι 12 καθώς περιλαμβάνει την απόδοση του αποθέματος για περίοδο 12 ετών.
Με αυτές τις δύο μεταβλητές, μπορούμε να υπολογίσουμε τον μέσο όρο του πληθυσμού για την επιστροφή των αποθεμάτων με τη βοήθεια του τύπου.
Ακολουθούν τα δεδομένα

Επομένως, η χρήση του παραπάνω μέσου πληροφοριών μπορεί να υπολογιστεί ως,

- µ = 224% / 12

Το παράδειγμα δείχνει ότι η μέση ή μέση απόδοση για την παρατηρούμενη τιμή είναι 19%.
Παράδειγμα # 2
Ας προσπαθήσουμε να αναλύσουμε την απόδοση ενός θεματικού αμοιβαίου κεφαλαίου τα τελευταία οκτώ χρόνια. Και οι αποδόσεις για το απόθεμα τα τελευταία δώδεκα χρόνια είναι 25%, 16%, 14%, 15%, 13%, 23%, 33% και 27%. Για να υπολογίσουμε το μέσο όρο για ολόκληρο τον πληθυσμό, πρέπει πρώτα να ανακαλύψουμε το άθροισμα όλων των παρατηρούμενων τιμών. Έτσι σε αυτό το παράδειγμα, το ∑X είναι 166% και ο αριθμός των παρατηρούμενων τιμών για τον πληθυσμό είναι 8 καθώς περιλαμβάνει την απόδοση του αμοιβαίου κεφαλαίου για περίοδο 8 ετών.
Με αυτές τις δύο μεταβλητές, μπορούμε να υπολογίσουμε τον μέσο όρο του πληθυσμού για την επιστροφή των αποθεμάτων με τη βοήθεια του τύπου.
Παρακάτω δίνονται δεδομένα για υπολογισμό

Επομένως, ο μέσος όρος μπορεί να υπολογιστεί ως,

- µ = 166% / 8

Το παράδειγμα δείχνει ότι η μέση ή μέση απόδοση για την παρατηρούμενη τιμή είναι 21%.
Παράδειγμα # 3
Ας ανακαλύψουμε τον μέσο πληθυσμό του βάρους των 15 μαθητών σε μια τάξη. Το βάρος κάθε μαθητή στην τάξη των 15 μαθητών σε kg είναι ως εξής 35, 36, 42, 40, 44, 45, 38, 42, 39, 42, 44, 45, 48, 42 και 40. Για να υπολογίστε τη μέση τιμή για ολόκληρο τον πληθυσμό, πρέπει πρώτα να ανακαλύψουμε το άθροισμα όλων των τιμών που παρατηρήθηκαν. Έτσι σε αυτό το παράδειγμα, το ∑X είναι 622 Kg και ο αριθμός των τιμών που παρατηρήθηκαν για τον πληθυσμό είναι 15 καθώς περιλαμβάνει το βάρος για 15 μαθητές.
Με αυτές τις δύο μεταβλητές, μπορούμε να υπολογίσουμε τον μέσο όρο του πληθυσμού για την επιστροφή των αποθεμάτων με τη βοήθεια του τύπου.
Ακολουθούν τα δεδομένα για τον υπολογισμό

Επομένως, με τη χρήση των παραπάνω πληροφοριών ο μέσος πληθυσμός μπορεί να υπολογιστεί ως,

- µ = 622/15

Το παράδειγμα δείχνει ότι η μέση ή μέση απόδοση για την παρατηρούμενη τιμή είναι 41,47
Συνάφεια και χρήση
Ο μέσος πληθυσμός είναι μια πολύ σημαντική στατιστική παράμετρος. Βοηθά στη γνώση του μέσου όρου των παραμέτρων του πληθυσμού. Ο μέσος όρος είναι σημαντικός καθώς χρησιμοποιείται στον υπολογισμό πολλών άλλων στατιστικών παραμέτρων όπως η διακύμανση, οι τυπικές αποκλίσεις και άλλες. Υπολογίζεται χρησιμοποιώντας την έννοια του αριθμητικού μέσου τύπου και αντιπροσωπεύει τον μέσο όρο ή τον μέσο όρο βάσει του οποίου μπορεί κανείς να συμπεράνει εάν μια παρατήρηση είναι υψηλή ή χαμηλή σε ολόκληρο τον πληθυσμό των παρατηρήσεων.