seychellesartprojects.org

Τύπος για τον υπολογισμό της δοκιμής Z στα στατιστικά στοιχεία

Η δοκιμή Z στα στατιστικά στοιχεία αναφέρεται στη δοκιμή υπόθεσης που χρησιμοποιείται για να προσδιοριστεί εάν τα δύο δείγματα μέσων που υπολογίζονται είναι διαφορετικά, σε περίπτωση που οι τυπικές αποκλίσεις είναι διαθέσιμες και το δείγμα είναι μεγάλο.

   Z = (x - μ) / ơ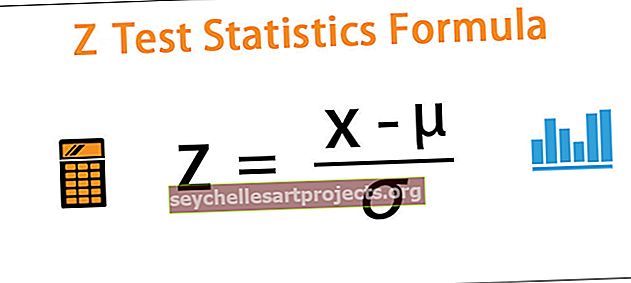      

όπου x = οποιαδήποτε τιμή από τον πληθυσμό

• μ = μέσος όρος πληθυσμού
• standard = τυπική απόκλιση πληθυσμού

Στην περίπτωση ενός δείγματος, ο τύπος των στατιστικών τιμών της δοκιμής z υπολογίζεται αφαιρώντας το μέσο όρο του δείγματος από την τιμή x και στη συνέχεια το αποτέλεσμα διαιρείται με την τυπική απόκλιση του δείγματος. Μαθηματικά, αντιπροσωπεύεται ως,

Z = (x - x_mean ) / s

που

• x = οποιαδήποτε τιμή από το δείγμα
• x_mean = μέσος όρος δείγματος
• s = τυπική απόκλιση δείγματος

Υπολογισμός δοκιμής Z (Βήμα προς βήμα)

Ο τύπος για στατιστικές δοκιμής z για έναν πληθυσμό προκύπτει ακολουθώντας τα ακόλουθα βήματα:

• Βήμα 1: Πρώτον, υπολογίστε τον μέσο πληθυσμό και την τυπική απόκλιση του πληθυσμού με βάση την παρατήρηση που καταγράφηκε στον μέσο όρο του πληθυσμού και κάθε παρατήρηση υποδηλώνεται με x _i . Ο συνολικός αριθμός παρατηρήσεων στον πληθυσμό υποδηλώνεται από τον Ν.

Μέσος πληθυσμός,

Τυπική απόκλιση πληθυσμού,

• Βήμα 2: Τέλος, τα στατιστικά στοιχεία της δοκιμής z υπολογίζονται αφαιρώντας τον μέσο όρο πληθυσμού από τη μεταβλητή και στη συνέχεια το αποτέλεσμα διαιρείται με την τυπική απόκλιση πληθυσμού όπως φαίνεται παρακάτω.

Z = (x - μ) / ơ

Ο τύπος για στατιστικά στοιχεία δοκιμής z για ένα δείγμα προέρχεται από τα ακόλουθα βήματα:

• Βήμα 1: Πρώτον, υπολογίστε τη μέση τιμή δείγματος και την τυπική απόκλιση δείγματος όπως παραπάνω. Εδώ, ο συνολικός αριθμός παρατηρήσεων στο δείγμα δηλώνεται με n έτσι ώστε n <N.

Μέσος δείγμα,

Τυπική απόκλιση δείγματος,

• Βήμα 2: Τέλος, τα στατιστικά στοιχεία της δοκιμής z υπολογίζονται αφαιρώντας το μέσο όρο δείγματος από την τιμή x και στη συνέχεια το αποτέλεσμα διαιρείται με την τυπική απόκλιση δείγματος όπως φαίνεται παρακάτω.

Z = (x - x_mean ) / s

Παραδείγματα

Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου δοκιμής τύπου φόρμουλας Excel εδώ - Πρότυπο δοκιμής φόρμουλας Excel

Παράδειγμα # 1

Ας υποθέσουμε ότι ένας πληθυσμός μαθητών σε ένα σχολείο που εμφανίστηκε για ένα τεστ τάξης. Η μέση βαθμολογία στη δοκιμή είναι 75 και η τυπική απόκλιση είναι 15. Προσδιορίστε τη βαθμολογία z-test του David που σκόραρε 90 στη δοκιμή.

Δεδομένος,

• Ο πληθυσμός σημαίνει, μ = 75
• Τυπική απόκλιση πληθυσμού, ơ = 15

Επομένως, τα στατιστικά στοιχεία της δοκιμής z μπορούν να υπολογιστούν ως,

Ζ = (90 - 75) / 15

Τα στατιστικά στοιχεία δοκιμής Z θα είναι -

• Ζ = 1

Επομένως, η βαθμολογία δοκιμής του David είναι μία τυπική απόκλιση πάνω από τη μέση βαθμολογία του πληθυσμού, δηλαδή σύμφωνα με τον πίνακα βαθμολογίας z, το 84,13% των μαθητών έχει λιγότερη βαθμολογία από τον David.

Παράδειγμα # 2

Ας πάρουμε το παράδειγμα 30 μαθητών που επιλέχθηκαν ως μέρος μιας ομάδας δείγματος που θα ερωτηθούν για να δουν πόσα μολύβια χρησιμοποιούνταν σε μια εβδομάδα. Προσδιορίστε το σκορ z-test για τον 3ο μαθητή βάσει των δοθέντων απαντήσεων: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Δεδομένος,

• x = 5, από την απάντηση του 3ου μαθητή, είναι 5
• Μέγεθος δείγματος, n = 30

Μέση δείγμα, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30

Μέση τιμή = 4.17

Τώρα, η τυπική απόκλιση δείγματος μπορεί να υπολογιστεί χρησιμοποιώντας τον παραπάνω τύπο.

ơ = 1,90

Επομένως, η βαθμολογία z-test για τον 3ο μαθητή μπορεί να υπολογιστεί ως,

Z = (x - x) / s

• Ζ = (5 –17) / 1,90
• Ζ = 0,44

Επομένως, η χρήση του 3ου μαθητή είναι 0,44 φορές η τυπική απόκλιση πάνω από τη μέση χρήση του δείγματος, δηλαδή σύμφωνα με τον πίνακα βαθμολογίας z, 67% οι μαθητές χρησιμοποιούν λιγότερα μολύβια από τον 3ο μαθητή.

Παράδειγμα # 3

Ας πάρουμε το παράδειγμα 30 μαθητών που επιλέχθηκαν ως μέρος μιας ομάδας δείγματος που θα ερωτηθούν για να δουν πόσα μολύβια χρησιμοποιούνταν σε μια εβδομάδα. Προσδιορίστε το σκορ z-test για τον 3ο μαθητή βάσει των δοθέντων απαντήσεων: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.

Παρακάτω δίνονται δεδομένα για τον υπολογισμό των Στατιστικών δοκιμών Z

Μπορείτε να ανατρέξετε στο δεδομένο φύλλο excel παρακάτω για τον λεπτομερή υπολογισμό των Στατιστικών δοκιμών Z.

Συνάφεια και χρήσεις

Είναι πολύ σημαντικό να κατανοήσουμε την έννοια των στατιστικών δοκιμών z επειδή χρησιμοποιείται συνήθως όποτε είναι αμφισβητήσιμο εάν ένα στατιστικό στοιχείο δοκιμής ακολουθεί μια φυσιολογική κατανομή βάσει της σχετικής μηδενικής υπόθεσης. Ωστόσο, πρέπει να θυμόμαστε ότι μια δοκιμή z χρησιμοποιείται μόνο όταν το μέγεθος του δείγματος είναι μεγαλύτερο από 30, διαφορετικά, χρησιμοποιείται η δοκιμή t.