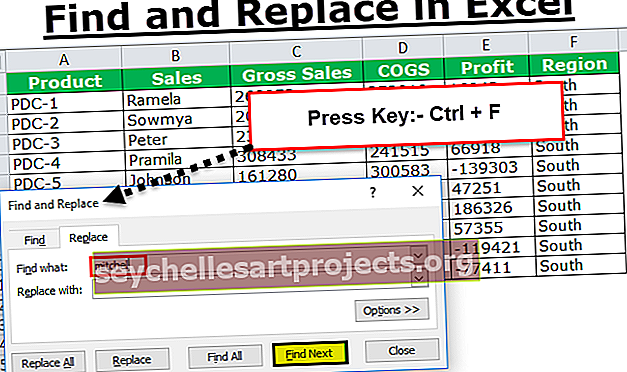
Lorenz Curve (Ορισμός, Παράδειγμα) | Τι είναι η Lorenz Curve στα Οικονομικά;
Ορισμός Lorenz Curve
Ο Lorenz Curve, που πήρε το όνομά του από τον Αμερικανό Οικονομολόγο Max O. Lorenz, είναι μια γραφική αναπαράσταση ενός μοντέλου οικονομικής ανισότητας. Η καμπύλη παίρνει λίγο το εκατοστημόριο του πληθυσμού στον άξονα Χ και τον σωρευτικό πλούτο στον άξονα Υ. Η συμπλήρωση αυτού του γραφήματος θα ήταν μια διαγώνια γραμμή σε γωνία 45⁰ από την προέλευση (σημείο συνάντησης του άξονα X & Y) που δείχνει την τέλεια κατανομή εισοδήματος ή πλούτου μεταξύ του πληθυσμού.
Κάτω από αυτήν την ευθεία διαγώνια γραμμή θα ήταν αυτή η πραγματική καμπύλη κατανομής Lorenz και η περιοχή που περικλείεται μεταξύ της γραμμής και αυτής της καμπύλης είναι η πραγματική μέτρηση της ανισότητας. Η περιοχή μεταξύ των δύο γραμμών που εκφράζεται ως αναλογία προς την περιοχή κάτω από την ευθεία γραμμή δίνει μια αναπαράσταση της ανισότητας και ονομάζεται συντελεστής Gini (αναπτύχθηκε από τον Ιταλό στατιστικολόγο Corrado Gini το έτος 1912).
Παράδειγμα καμπύλης Lorenz
Ακολουθεί το παράδειγμα για την κατανόηση της καμπύλης Lorenz με τη βοήθεια ενός γραφήματος.
Ας εξετάσουμε μια οικονομία με τις ακόλουθες στατιστικές πληθυσμού και εισοδήματος:

Και για τη γραμμή της τέλειας ισότητας, ας εξετάσουμε αυτόν τον πίνακα:

Ας δούμε τώρα πώς φαίνεται ένα γράφημα για αυτά τα δεδομένα:

Όπως μπορούμε να δούμε, υπάρχουν δύο γραμμές στο γράφημα της καμπύλης Lorenz, η καμπύλη κόκκινη γραμμή και η ευθεία μαύρη γραμμή. Η μαύρη γραμμή αντιπροσωπεύει τη φανταστική γραμμή που ονομάζεται γραμμή ισότητας, δηλαδή το ιδανικό γράφημα όταν το εισόδημα ή ο πλούτος κατανέμεται εξίσου στον πληθυσμό. Η κόκκινη καμπύλη, η καμπύλη Lorenz, την οποία συζητάμε, αντιπροσωπεύει την πραγματική κατανομή του πλούτου μεταξύ του πληθυσμού.
Ως εκ τούτου, μπορούμε να πούμε ότι η καμπύλη Lorenz είναι η γραφική μέθοδος μελέτης διασποράς. Ο συντελεστής Gini, επίσης γνωστός ως δείκτης Gini, μπορεί να υπολογιστεί ως εξής. Ας υποθέσουμε ότι στην περιοχή του γραφήματος μεταξύ της καμπύλης Lorenz και η γραμμή αντιπροσωπεύεται από το A1 και η γραμμή κάτω από την καμπύλη αντιπροσωπεύεται από το A2 . Ετσι,
Συντελεστής Gini = A1 / (A1 + A2)Ο συντελεστής Gini βρίσκεται μεταξύ 0 και 1. 0 είναι η περίπτωση όπου υπάρχει τέλεια ισότητα και 1 είναι η περίπτωση όπου υπάρχει τέλεια ανισότητα. Όσο υψηλότερη είναι η έκταση που περικλείεται μεταξύ των δύο γραμμών αντιπροσωπεύει μεγαλύτερη ανισότητα στην οικονομία.
Με αυτό, μπορούμε να πούμε ότι για τη μέτρηση της εισοδηματικής ανισότητας, υπάρχουν δύο δείκτες:
- Η καμπύλη Lorenz είναι ο οπτικός δείκτης και
- Ο συντελεστής Gini είναι ο μαθηματικός δείκτης.
Η ανισότητα εισοδήματος είναι ένα πιεστικό ζήτημα σε όλο τον κόσμο. Λοιπόν, ποιοι είναι οι λόγοι για την ανισότητα σε μια οικονομία;
- Διαφθορά
- Εκπαίδευση
- Φόρος
- Διαφορές φύλου
- Πολιτισμός
- Διακρίσεις φυλών και ηθοποιών
- Η διαφορά στις προτιμήσεις αναψυχής και κινδύνων.
Λόγοι για εισοδηματική ανισότητα
- Θα πρέπει να εξεταστεί η κατανομή των οικονομικών χαρακτηριστικών στον πληθυσμό.
- Αναλύοντας πώς οι διαφορές δημιουργούν διαφορετικά αποτελέσματα όσον αφορά το εισόδημα.
- Μια χώρα μπορεί να έχει υψηλό βαθμό ανισότητας λόγω -
- Η μεγάλη ανισότητα σε αυτά τα χαρακτηριστικά σε ολόκληρο τον πληθυσμό.
- Αυτά τα χαρακτηριστικά δημιουργούν τεράστιες επιπτώσεις στο ποσό εισοδήματος που κερδίζει ένα άτομο.
Χρήσεις της καμπύλης Lorenz
- Μπορεί να χρησιμοποιηθεί για να δείξει την αποτελεσματικότητα μιας κυβερνητικής πολιτικής για την αναδιανομή του εισοδήματος. Ο αντίκτυπος μιας συγκεκριμένης πολιτικής που παρουσιάζεται μπορεί να φανεί με τη βοήθεια της καμπύλης Lorenz, πώς η καμπύλη έχει προχωρήσει πιο κοντά στην τέλεια γραμμή ισότητας μετά την εφαρμογή αυτής της πολιτικής.
- Είναι μια από τις απλούστερες αναπαραστάσεις ανισότητας.
- Είναι πολύ χρήσιμο στη σύγκριση της μεταβλητότητας δύο ή περισσότερων κατανομών.
- Δείχνει την κατανομή του πλούτου μιας χώρας μεταξύ των διαφορετικών ποσοστών του πληθυσμού με τη βοήθεια ενός γραφήματος που βοηθά πολλές επιχειρήσεις στη δημιουργία των βάσεων στόχων τους.
- Βοηθά στην επιχειρηματική μοντελοποίηση.
- Μπορεί να χρησιμοποιηθεί κυρίως λαμβάνοντας συγκεκριμένα μέτρα για την ανάπτυξη των ασθενέστερων τμημάτων της οικονομίας.
Περιορισμοί
- Αυτό μπορεί να μην είναι πάντα αυστηρό για ένα πεπερασμένο επίπεδο πληθυσμού.
- Το μέτρο ισότητας που φαίνεται μπορεί να είναι παραπλανητικό.
- Όταν συγκρίνονται δύο καμπύλες Lorenz και τέμνονται τέτοιες δύο καμπύλες, δεν είναι δυνατόν να εξακριβωθεί ποια κατανομή αντιπροσωπεύεται από τις καμπύλες εμφανίζει μεγαλύτερη ανισότητα.
- Η διακύμανση του εισοδήματος κατά τη διάρκεια του κύκλου ζωής ενός ατόμου αγνοείται από την καμπύλη Lorenz κατά τον προσδιορισμό της ανισότητας.
συμπέρασμα
Για να ολοκληρώσουμε συνοψίζοντας όσα έχουμε μάθει, που παρουσιάστηκε πριν από περισσότερα από 100 χρόνια, η καμπύλη Lorenz παρέχει μια έμφυτη και πλήρη κατανόηση της κατανομής εισοδήματος και παρέχει τη βάση για μετρήσεις ανισότητας μέσω του δείκτη Gini.
Η καμπύλη καθορίζει τη σχέση μεταξύ των σωρευτικών τμημάτων του εισοδήματος όπως λαμβάνεται από τον σωρευτικό πληθυσμό όταν ο εισοδηματικός πληθυσμός είναι διατεταγμένος σε αύξουσα σειρά.
Ο βαθμός στον οποίο η καμπύλη διογκώνεται προς τα κάτω κάτω από την ευθεία διαγώνια γραμμή που ονομάζεται γραμμή ισότητας υποδηλώνει το βαθμό ανισότητας κατανομής. Αυτό σημαίνει ότι η καμπύλη θα υποκλίνεται πάντα προς τα κάτω έως ότου υπάρξει ανισότητα στην οικονομία.
Αν και θεωρείται το απλούστερο μεταξύ όλων των άλλων μέτρων ανισοτήτων, το γράφημα μπορεί να είναι παραπλανητικό και μπορεί να μην παράγει πάντα ακριβή αποτελέσματα.