Τύπος παραλλαγής πληθυσμού | Υπολογισμός βήμα προς βήμα | Παραδείγματα
Τύπος για τον υπολογισμό της διακύμανσης του πληθυσμού
Ο τύπος πληθυσμιακής διακύμανσης είναι ένα μέτρο από τις μέσες αποστάσεις των δεδομένων πληθυσμού και υπολογίζεται με την εύρεση του μέσου όρου του πληθυσμού και η διακύμανση υπολογίζεται με το άθροισμα του τετραγώνου των μεταβλητών μείον τον μέσο όρο που διαιρείται με έναν αριθμό παρατηρήσεων στον πληθυσμό.
Η διακύμανση του πληθυσμού είναι ένα μέτρο της διάδοσης των δεδομένων του πληθυσμού. Ως εκ τούτου, η διακύμανση του πληθυσμού μπορεί να οριστεί ως ο μέσος όρος των αποστάσεων από κάθε σημείο δεδομένων σε έναν συγκεκριμένο πληθυσμό έως τον μέσο όρο, τετράγωνο και δείχνει πώς τα σημεία δεδομένων κατανέμονται στον πληθυσμό. Η διακύμανση του πληθυσμού είναι ένα σημαντικό μέτρο διασποράς που χρησιμοποιείται στις στατιστικές. Οι στατιστικολόγοι υπολογίζουν τη διακύμανση για να καθορίσουν πώς οι μεμονωμένοι αριθμοί σε ένα σύνολο δεδομένων σχετίζονται μεταξύ τους.
Κατά τον υπολογισμό της διακύμανσης του πληθυσμού, η διασπορά υπολογίζεται με αναφορά στον μέσο πληθυσμό. Ως εκ τούτου, πρέπει να μάθουμε τον μέσο όρο του πληθυσμού για να υπολογίσουμε τη διακύμανση του πληθυσμού. Μία από τις πιο δημοφιλείς ειδοποιήσεις για τη διακύμανση του πληθυσμού είναι σ2. Αυτό προφέρεται ως sigma squared.
Η διακύμανση πληθυσμού μπορεί να υπολογιστεί χρησιμοποιώντας τον ακόλουθο τύπο:


που
- σ2 είναι η διακύμανση του πληθυσμού,
- x 1, x 2 , x 3, … ..x n είναι οι παρατηρήσεις
- N είναι ο αριθμός των παρατηρήσεων,
- μ είναι ο μέσος όρος του συνόλου δεδομένων
Βήμα προς βήμα Υπολογισμός Διακύμανσης Πληθυσμού
Ο τύπος διακύμανσης πληθυσμού μπορεί να υπολογιστεί χρησιμοποιώντας τα ακόλουθα πέντε απλά βήματα:
- Βήμα 1: Υπολογίστε τον μέσο όρο (μ) των δεδομένων δεδομένων. Για τον υπολογισμό του μέσου όρου, προσθέστε όλες τις παρατηρήσεις και μετά διαιρέστε το με τον αριθμό των παρατηρήσεων (Ν).
- Βήμα 2: Δημιουργήστε ένα τραπέζι. Λάβετε υπόψη ότι η κατασκευή ενός πίνακα δεν είναι υποχρεωτική, αλλά η παρουσίασή του σε μορφή πίνακα θα διευκολύνει τους υπολογισμούς. Στην πρώτη στήλη, γράψτε κάθε παρατήρηση (x 1, x 2 , x 3, … ..x n ).
- Βήμα 3: Στη δεύτερη στήλη, γράψτε την απόκλιση κάθε παρατήρησης από το μέσο όρο (x i - μ).
- Βήμα 4: Στην τρίτη στήλη, γράψτε το τετράγωνο κάθε παρατήρησης από το μέσο όρο (x i - μ) 2. Με άλλα λόγια, τετραγωνίστε κάθε έναν από τους αριθμούς που λαμβάνονται στη στήλη 2.
- Βήμα 5: Στη συνέχεια πρέπει να προσθέσουμε τους αριθμούς που λαμβάνονται στην τρίτη στήλη. Βρείτε το άθροισμα των τετραγώνων αποκλίσεων και διαιρέστε το άθροισμα που λαμβάνεται με τον αριθμό των παρατηρήσεων (N). Αυτό θα μας βοηθήσει να αποκτήσουμε
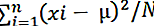 ποια είναι η διακύμανση του πληθυσμού.
ποια είναι η διακύμανση του πληθυσμού.
Παραδείγματα
Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου Formula Excel Formulation Variance Formula - Πρότυπο Excel Population Variance Formula ExcelΠαράδειγμα # 1
Υπολογίστε τη διακύμανση του πληθυσμού από τις ακόλουθες 5 παρατηρήσεις: 50, 55, 45, 60, 40.
Λύση:
Χρησιμοποιήστε τα ακόλουθα δεδομένα για τον υπολογισμό της διακύμανσης του πληθυσμού.

Υπάρχουν συνολικά 5 παρατηρήσεις. Ως εκ τούτου, N = 5.
µ = (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
Έτσι, ο υπολογισμός της διακύμανσης του πληθυσμού σ2 μπορεί να γίνει ως εξής-


σ2 = 250/5
Πληθυσμός πληθυσμού σ2 θα είναι-

Ποικιλία πληθυσμού (σ2) = 50
Η διακύμανση του πληθυσμού είναι 50.
Παράδειγμα # 2
Η XYZ Ltd. είναι μια μικρή εταιρεία και απαρτίζεται από μόνο 6 υπαλλήλους. Ο Διευθύνων Σύμβουλος πιστεύει ότι δεν πρέπει να υπάρχει μεγάλη διασπορά στους μισθούς αυτών των εργαζομένων. Για το σκοπό αυτό, θέλει να υπολογίσετε τη διαφορά αυτών των μισθών. Οι μισθοί αυτών των υπαλλήλων είναι όπως παρακάτω. Υπολογίστε τη διακύμανση των μισθών για τον Διευθύνοντα Σύμβουλο.
Λύση:
Χρησιμοποιήστε τα ακόλουθα δεδομένα για τον υπολογισμό της διακύμανσης του πληθυσμού.

Υπάρχουν συνολικά 6 παρατηρήσεις. Ως εκ τούτου, Ν = 6.
= (30 + 27 + 20 + 40 + 32 + 31) / 6 = 180/6 = 30 $
Έτσι, ο υπολογισμός της διακύμανσης του πληθυσμού σ2 μπορεί να γίνει ως εξής-


σ2 = 214/6
Πληθυσμός πληθυσμού σ2 θα είναι-

Ποικιλία πληθυσμού (σ2) = 35,67
Η διακύμανση των μισθών είναι 35,67.
Παράδειγμα # 3
Η Sweet Juice Ltd παράγει διαφορετικές γεύσεις χυμού. Το Τμήμα Διαχείρισης αγοράζει 7 μεγάλα δοχεία για την αποθήκευση αυτού του χυμού στο εργοστάσιο. Το Τμήμα Ελέγχου Ποιότητας αποφάσισε ότι θα απορρίψει τα εμπορευματοκιβώτια εάν η διακύμανση των εμπορευματοκιβωτίων είναι πάνω από 10. Δεδομένου ότι τα βάρη των 7 εμπορευματοκιβωτίων σε kg: 105, 100, 102, 95, 100, 98 και 107. Παρακαλούμε ενημερώστε την Ποιότητα Ελέγξτε το Τμήμα εάν πρέπει να απορρίψει τα δοχεία
Λύση:
Χρησιμοποιήστε τα ακόλουθα δεδομένα για τον υπολογισμό της διακύμανσης του πληθυσμού.

Υπάρχουν συνολικά 7 παρατηρήσεις. Ως εκ τούτου, N = 7
= (105 + 100 + 102 + 95 + 100 + 98 + 107) / 7 = 707/7 = 10
Έτσι, ο υπολογισμός της διακύμανσης του πληθυσμού σ2 μπορεί να γίνει ως εξής-


σ2 = 100/7
Πληθυσμός πληθυσμού σ2 θα είναι-

Ποικιλία πληθυσμού (σ2) = 14,29
Δεδομένου ότι η διακύμανση (14.29) είναι μεγαλύτερη από το όριο των 10 που αποφασίστηκε από το Τμήμα Ελέγχου Ποιότητας, τα δοχεία πρέπει να απορριφθούν.
Παράδειγμα # 4
Η ομάδα διαχείρισης ενός νοσοκομείου Sagar Healthcare κατέγραψε ότι 8 μωρά γεννήθηκαν την πρώτη εβδομάδα του Μαρτίου 2019. Ο γιατρός ήθελε να αξιολογήσει την υγεία των μωρών καθώς και τη διακύμανση των υψών. Τα ύψη αυτών των μωρών έχουν ως εξής: 48 cm, 47 cm, 50 cm, 53 cm, 50 cm, 52 cm, 51 cm, 60 cm. Υπολογίστε τη διακύμανση του ύψους αυτών των 8 μωρών.
Λύση:
Χρησιμοποιήστε τα ακόλουθα δεδομένα για τον υπολογισμό της διακύμανσης του πληθυσμού.

Έτσι, ο υπολογισμός της διακύμανσης του πληθυσμού σ2 μπορεί να γίνει ως εξής-

Στο Excel, υπάρχει ένας ενσωματωμένος τύπος για διακύμανση πληθυσμού που μπορεί να χρησιμοποιηθεί για τον υπολογισμό της διακύμανσης πληθυσμού μιας ομάδας αριθμών. Επιλέξτε ένα κενό κελί και πληκτρολογήστε αυτόν τον τύπο = VAR.P (B2: B9). Εδώ, το B2: B9 είναι το εύρος των κελιών από τα οποία θέλετε να υπολογίσετε τη διακύμανση του πληθυσμού.
Πληθυσμός πληθυσμού σ2 θα είναι-

Ποικιλία πληθυσμού (σ2) = 13,98
Συνάφεια και χρήση
Η διακύμανση του πληθυσμού χρησιμοποιείται ως μέτρο διασποράς. Ας εξετάσουμε δύο ομάδες πληθυσμού με τον ίδιο μέσο και αριθμό παρατηρήσεων. Το σύνολο δεδομένων 1 αποτελείται από 5 αριθμούς - 55, 50, 45, 50 και 50. Το σύνολο δεδομένων 2 αποτελείται από 10, 50, 85, 90 και 15. Και τα δύο σύνολα δεδομένων έχουν τον ίδιο μέσο όρο, που είναι 50. Αλλά, Στο σύνολο δεδομένων 1, οι τιμές είναι το ένα κοντά στο άλλο, ενώ το σύνολο δεδομένων 2 έχει διασπαρμένες τιμές. Η διακύμανση δίνει ένα επιστημονικό μέτρο αυτής της εγγύτητας / διασποράς. Το σύνολο δεδομένων 1 έχει διακύμανση μόνο 10, ενώ το σύνολο δεδομένων 2 έχει τεράστια διακύμανση 1130. Έτσι, μια μεγάλη διακύμανση δείχνει ότι οι αριθμοί απέχουν πολύ από τον μέσο όρο και ο ένας από τον άλλο. Μια μικρή διακύμανση δείχνει ότι οι αριθμοί είναι κοντά ο ένας στον άλλο.
Η διακύμανση χρησιμοποιείται στον τομέα της διαχείρισης χαρτοφυλακίου κατά την εκτέλεση της κατανομής περιουσιακών στοιχείων. Οι επενδυτές υπολογίζουν τη διακύμανση των αποδόσεων περιουσιακών στοιχείων για να καθορίσουν τα βέλτιστα χαρτοφυλάκια βελτιστοποιώντας τις δύο βασικές παραμέτρους - απόδοση και αστάθεια Η μεταβλητότητα που μετράται με διακύμανση είναι ένα μέτρο του κινδύνου μιας συγκεκριμένης χρηματοοικονομικής ασφάλειας.

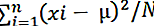 ποια είναι η διακύμανση του πληθυσμού.
ποια είναι η διακύμανση του πληθυσμού.