Τύπος συνεχούς σύνθεσης

Τύπος συνεχούς σύνθεσης | Παραδείγματα | Αριθμομηχανή

Τι είναι η συνεχής συνένωση;

Η συνεχής συνένωση υπολογίζει το όριο στο οποίο μπορεί να επιτύχει το σύνθετο επιτόκιο συνθέτοντας συνεχώς για αόριστο χρονικό διάστημα αυξάνοντας έτσι το στοιχείο τόκου και τελικά την αξία χαρτοφυλακίου των συνολικών επενδύσεων

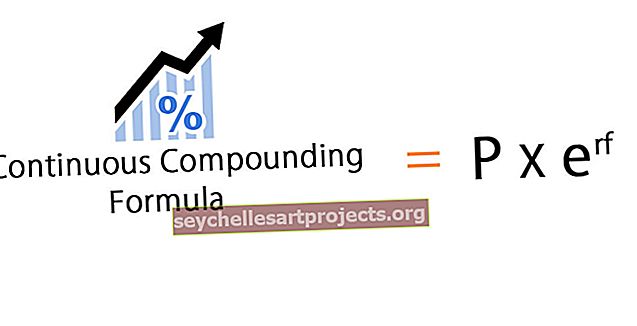
Ο τύπος συνεχούς σύνθεσης καθορίζει τους κερδισμένους τόκους που αναμιγνύονται επανειλημμένα για απεριόριστο χρονικό διάστημα.

που,

P = Κύριο ποσό (παρούσα αξία)
t = Ώρα
r = Επιτόκιο

Ο υπολογισμός προϋποθέτει συνεχή συνένωση σε άπειρο αριθμό χρονικών περιόδων. Δεδομένου ότι η χρονική περίοδος είναι άπειρη, ο εκθέτης βοηθά στον πολλαπλασιασμό της τρέχουσας επένδυσης. Αυτό πολλαπλασιάζεται με την τρέχουσα τιμή και ώρα. Παρά τον μεγάλο αριθμό επενδύσεων, η διαφορά στο συνολικό επιτόκιο που κερδίζεται μέσω της συνεχούς σύνθετης σύνθεσης excel είναι μικρότερη σε σύγκριση με την παραδοσιακή ένωση που θα εξεταστεί μέσω παραδειγμάτων.

Παράδειγμα

Ας αναλύσουμε μερικές από τις περιπτώσεις:

Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου συνεχούς σύνθεσης του Excel εδώ - Πρότυπο συνεχούς σύνθεσης του Excel

Εάν μια αρχική επένδυση 1.000 $ επενδύεται σε επιτόκιο 8% ετησίως με συνεχή επιδείνωση, πόσο θα ήταν στον λογαριασμό μετά από 5 χρόνια;

P = 1.000 $, r = 8%, n = 5 έτη
FV = P * e rt = 1.000 * e (0.08) (5) = 1.000 * e (0.40) [Ο εκθέτης του 0.4 είναι 1.491] = 1.000 * 1.491
= 1,491,8 $

Ας υπολογίσουμε τις επιδράσεις του ίδιου στην κανονική σύνθεση

Ετήσια σύνθεση:

FV = 1.000 * (1 + 0.08) ^ 1 = 1.080 $

Εξαμηνιαία συνένωση:

FV = 1.000 * [(1 + 0,08 / 2)] ^ 2
= 1.000 * (1.04) ^ 2
= 1.000 * 1.0816 = 1.081.60 $

Τριμηνιαία συνένωση:

FV = 1.000 * [(1 + 0,08 / 4)] ^ 4
= 1.000 * (1.02) ^ 4
= 1.000 * 1.08243
= 1.082,43 $

Μηνιαία συνένωση:

FV = 1.000 * [(1 + 0,08 / 12)] 12
= 1.000 * (1.006) ^ 4
= 1.000 * 1.083
= 1.083 $

Συνεχής συνένωση:

FV = 1.000 * e 0,08
= 1.000 * 1.08328
= 1.083,29 $

Όπως μπορεί να παρατηρηθεί από το παραπάνω παράδειγμα, οι τόκοι που προκύπτουν από τη συνεχή συνένωση είναι 83,28 $ που είναι μόνο 0,28 $ περισσότερο από τη μηνιαία σύνθεση.

Ένα άλλο παράδειγμα μπορεί να πει ότι ένας Λογαριασμός Ταμιευτηρίου πληρώνει ετήσιο τόκο 6%, σε συνδυασμό συνεχώς. Πόσο πρέπει να επενδύσετε τώρα για να έχετε 100.000 $ στο λογαριασμό 30 χρόνια από τώρα;

FV = PV * ert
PV = FV * e - rt
PV = 100.000 * e - (0,06) (30)
PV = 100.000 * e - (1,80)
PV = 100.000 * 0,1652988
PV = 16.529,89 $

Έτσι, εάν ένα ποσό 16.530 $ (στρογγυλοποιημένο) επενδυθεί σήμερα, θα αποφέρει 100.000 $ μετά από 30 χρόνια με το δεδομένο επιτόκιο.

Ένα άλλο παράδειγμα μπορεί να είναι εάν ένας καρχαρίας δανείου χρεώνει τόκους 80%, σε συνεχή βάση, ποιο θα είναι το πραγματικό ετήσιο επιτόκιο;

Επιτόκιο = e 0,80 - 1
= 2.2255 - 1 = 1.22.55 = 122.55 %

Χρήσεις

Αντί της συνεχιζόμενης συγκέντρωσης τόκων σε μηνιαία, τριμηνιαία ή ετήσια βάση, αυτό θα επανεπενδύσει αποτελεσματικά τα κέρδη διαρκώς.
Η επίδραση του επιτοκίου επιτρέπει την επανεπένδυση επιτρέποντας έτσι σε έναν επενδυτή να κερδίζει με εκθετικό επιτόκιο
Αυτό καθορίζει ότι δεν θα κερδίσει μόνο το κύριο ποσό αλλά θα συνεχίσει να πολλαπλασιάζεται η συνεχής επιμέτρηση του επιτοκίου.

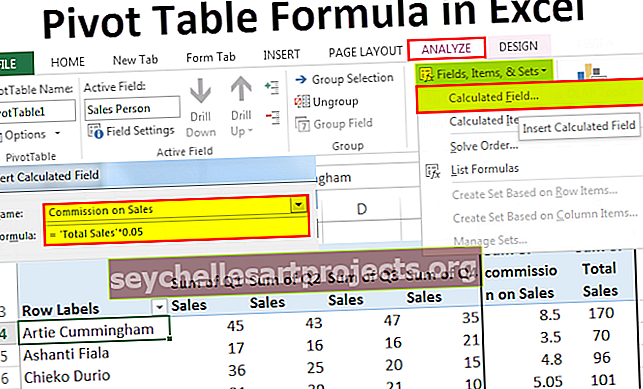
Υπολογιστής συνεχούς σύνθεσης

Μπορείτε να χρησιμοποιήσετε την ακόλουθη αριθμομηχανή

Π
ρ
τ
Τύπος συνεχούς σύνθεσης =

Τύπος συνεχούς σύνθεσης =	P xe (rxt) =
	0 * e (0 * 0) =	0