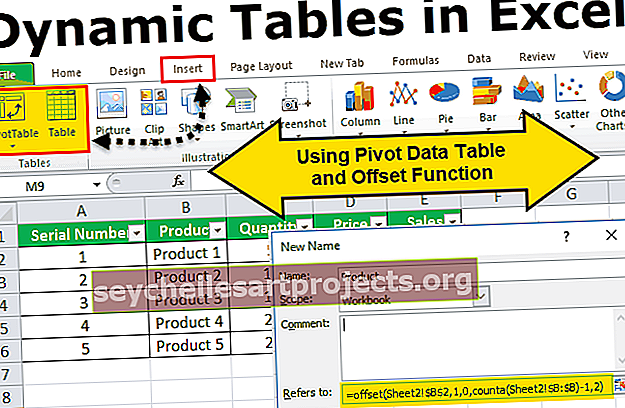
Διακύμανση έναντι τυπικής απόκλισης | Κορυφαίες 6 διαφορές (Infographics)
Διαφορά μεταξύ διακύμανσης και τυπικής απόκλισης
Η διακύμανση είναι μια μέθοδος εύρεσης ή απόκτησης του μέτρου μεταξύ των μεταβλητών που διαφέρουν μεταξύ τους, ενώ η τυπική απόκλιση μάς δείχνει πώς το σύνολο δεδομένων ή οι μεταβλητές διαφέρουν από τη μέση ή τη μέση τιμή από το σύνολο δεδομένων.
Η διακύμανση συμβάλλει στην εύρεση της κατανομής δεδομένων σε έναν πληθυσμό από μια μέση τιμή και η τυπική απόκλιση βοηθά επίσης να γνωρίζουμε την κατανομή των δεδομένων στον πληθυσμό, αλλά η τυπική απόκλιση δίνει περισσότερη σαφήνεια σχετικά με την απόκλιση των δεδομένων από έναν μέσο όρο.

Τύπος
Ακολουθούν οι τύποι διακύμανσης και τυπικής απόκλισης.

Ενώ
- Το σ2 είναι διακύμανση
- Το Χ είναι μεταβλητό
- μ είναι μέσος όρος
- N είναι ο συνολικός αριθμός μεταβλητών.
Η τυπική απόκλιση είναι η τετραγωνική ρίζα της διακύμανσης.
Παράδειγμα
Φανταστείτε ένα παιχνίδι που λειτουργεί έτσι
Περίπτωση-1
Τράβετε ένα φύλλο από μια συνηθισμένη τράπουλα
- Εάν ισοπατήσετε 7 θα κερδίσετε INR 2000 / -
- Εάν επιλέξετε άλλη κάρτα εκτός από 7, θα δώσετε 100 INR / -

Περίπτωση-2
- Εάν τραβήξετε 7, θα κερδίσετε 1,22.000 INR / -
- Εάν επιλέξετε άλλη κάρτα εκτός από 7, θα δώσετε 10,100 INR / - INR
Ας υποθέσουμε ότι έχετε παίξει ένα παιχνίδι 52.000 φορές.

Για μια διακριτή τυχαία μεταβλητή, η διακύμανση είναι

Όπου το Pi είναι η πιθανότητα του αποτελέσματος.
Το μέσο κέρδος ανά παιχνίδι και για τις δύο περιπτώσεις είναι Rs.61.54 ποιο παιχνίδι θα θέλατε να παίξετε καλά, υπάρχει ένα συγκεκριμένο μέσο που βοηθά στη λήψη απόφασης, δηλαδή πρέπει να υπολογίσουμε τη διακύμανση και την τυπική απόκλιση

Πρέπει να μετρήσουμε την κανονική απόκλιση από την αναμενόμενη τιμή και ένα κοινό μέτρο είναι το Variance. Η διακύμανση μιας υπόθεσης -1 είναι πολύ μικρότερη από τη διακύμανση μιας υπόθεσης -2 που σημαίνει ότι τα δεδομένα στην περίπτωση -2 διέδωσαν τη μέση τιμή, δηλαδή Rs 64,54, οπότε το παιχνίδι Case-1 έχει μικρότερο κίνδυνο από το παιχνίδι Case-2.
Στα χρηματοοικονομικά μιλήσαμε για την αστάθεια για παράδειγμα των μετοχών που σημαίνει ότι τα μεγάλα σοκ στην επιστροφή χρηματοοικονομικών περιουσιακών στοιχείων τείνουν να ακολουθούνται από μεγάλα σοκ και μικρά σοκ στην επιστροφή χρηματοοικονομικών περιουσιακών στοιχείων τείνουν να ακολουθούνται από μικρά σοκ
Infographics διακύμανσης έναντι τυπικής απόκλισης
Ας δούμε τις κορυφαίες διαφορές μεταξύ Variance έναντι Standard Deviation.

Βασικές διαφορές
Οι βασικές διαφορές είναι οι εξής:
- Η διακύμανση δίνει μια κατά προσέγγιση ιδέα της μεταβλητότητας των δεδομένων. Το 68% των τιμών κυμαίνεται μεταξύ τυπικής απόκλισης +1 και -1 από τον μέσο όρο. Αυτό σημαίνει ότι η τυπική απόκλιση δίνει περισσότερες λεπτομέρειες.
- Η διακύμανση χρησιμοποιείται για να μάθει για την προγραμματισμένη και πραγματική συμπεριφορά με κάποιο βαθμό αβεβαιότητας. Η τυπική απόκλιση χρησιμοποιείται για τη στατιστική δοκιμή για να μάθει για τη σχέση που υπάρχει μεταξύ δύο συνόλων μεταβλητής
- Η διακύμανση μετρά την κατανομή δεδομένων σε έναν πληθυσμό γύρω από την κεντρική τιμή. Η τυπική απόκλιση μετρά την κατανομή δεδομένων σε σχέση με την κεντρική τιμή
- Άθροισμα δύο παραλλαγών (var (A + B) ≥ var (A) + var (B). Επομένως η διακύμανση δεν είναι συνεκτική. Άθροισμα δύο τυπικών απόκλισης sd (A + B) ≤ sd (A) + sd (B) έτσι , Η τυπική απόκλιση είναι συνεκτική. Δίνει την ιδέα της ασυμμετρίας των δεδομένων. Η τιμή της ασυμμετρίας της συμμετρικής κατανομής κυμαίνεται μεταξύ -1> 0> 1.
- Ο γεωμετρικός μέσος είναι πιο ευαίσθητος στη διακύμανση από τον αριθμητικό μέσο. Μια γεωμετρική τυπική απόκλιση χρησιμοποιείται για να βρει τα όρια του διαστήματος εμπιστοσύνης σε έναν πληθυσμό.
Συγκριτικός πίνακας διακύμανσης έναντι τυπικής απόκλισης
| Διαφορά | Τυπική απόκλιση | |
| Μέσες τετραγωνικές διαφορές από το μέσο όρο | Η τετραγωνική ρίζα της διακύμανσης | |
| Μετρά τη διασπορά εντός του συνόλου δεδομένων | μετρά την εξάπλωση γύρω από το μέσο όρο | |
| Η διακύμανση δεν είναι υπο-πρόσθετο | Ένα μέτρο διασποράς για συμμετρικές διανομές χωρίς ακραίες τιμές. | |
| Η διακύμανση μετρά επίσης την μεταβλητότητα των δεδομένων ενός πληθυσμού | Η τυπική απόκλιση, στα χρηματοοικονομικά, ονομάζεται συχνά μεταβλητότητα | |
| Η διακύμανση μετρά πόσο μακριά διαφέρει το αποτέλεσμα από το μέσο. | Η τυπική απόκλιση μετρά πόσο μακριά είναι η κανονική τυπική απόκλιση από την αναμενόμενη τιμή. Η τυπική απόκλιση μπορεί να χρησιμεύσει ως μέτρο αβεβαιότητας | |
| Στα Χρηματοοικονομικά, βοηθά στη μέτρηση της πραγματικής απόκλισης απόδοσης από το πρότυπο. | Η τυπική απόκλιση είναι ένα χρήσιμο εργαλείο για τη λήψη απόφασης σχετικά με την επένδυση σε μετοχές, αμοιβαία κεφάλαια κ.λπ. επειδή μετρά τον κίνδυνο που σχετίζεται με την αστάθεια της αγοράς. | |
| Διορθωτικά μέτρα μπορούν να ληφθούν γνωρίζοντας το Variance. | Η διαδικασία ανάλυσης κινδύνου είναι η ανάλυση και ερμηνεία του αποτελέσματος που συλλέχθηκε κατά τον υπολογισμό της τυπικής απόκλισης διαφόρων αποθεμάτων και το αποτέλεσμα αναλύεται για να ληφθεί μια αποτελεσματική απόφαση σχετικά με την επένδυση κεφαλαίων. |
Χρήσεις διακύμανσης και τυπική απόκλιση
Παράδειγμα προσδιορισμού τιμολόγησης πετρελαίου
- Ποια θα είναι η τιμή του λαδιού σε ένα έτος; Όχι μια εκτίμηση τιμής. Η πιθανότητα να είναι χαμηλή ή υψηλή
- Διακύμανση καθυστερήσεων, διακύμανση απορριμμάτων / επισκευής, διακύμανση πραγματικών ωρών πτήσης έναντι προγραμματισμένης
- Η επόμενη τιμή επιστρέφει στον μέσο όρο ή εξαρτάται μόνο από την τελευταία τιμή;
- Το επόμενο ποσό της ζήτησης επιστρέφει στο μέσο όρο ή εξαρτάται μόνο από το τελευταίο ποσό της ζήτησης;



Προβλεπόμενο ποσό για αρκετές περιόδους (τιμή λαδιού για 20 μήνες)

* Το γράφημα δημιουργείται λαμβάνοντας υπόψη τα δεδομένα ενός έτους, ωστόσο στον πίνακα τα δεδομένα που εμφανίζονται είναι μόνο για 6 μήνες και η τιμή επιλέγεται τυχαία, η οποία μπορεί να μην είναι η ίδια με τα δεδομένα αγοράς της τιμής του πετρελαίου.
Τελικές σκέψεις
Τόσο η διακύμανση όσο και η τυπική απόκλιση μετρούν την εξάπλωση των δεδομένων από το μέσο της σημείο. Βοηθά στον προσδιορισμό του κινδύνου στην επένδυση του αμοιβαίου κεφαλαίου, στο απόθεμα κ.λπ. Είναι ένα χρήσιμο εργαλείο που χρησιμοποιείται στην πρόγνωση του καιρού για μεταβολή της θερμοκρασίας κατά τη διάρκεια της περιόδου και το Monte Carlo Simulation για την εκτίμηση του κινδύνου του έργου.