Βάλτε φόρμα ισοτιμίας κλήσης | Υπολογισμός βήμα προς βήμα με παραδείγματα
Τι είναι ο τύπος ισοτιμίας Put-Call;
Ο τύπος Put-Call Parity δηλώνει ότι η απόδοση από την κατοχή μιας βραχυπρόθεσμης θέσης και μιας επιλογής μακράς κλήσης για ένα απόθεμα θα πρέπει να παρέχει την ίδια απόδοση όπως παρέχεται κρατώντας ένα προθεσμιακό συμβόλαιο για το ίδιο απόθεμα. Η αρχή ισχύει όταν τόσο οι επιλογές όσο και οι προθεσμιακές συμβάσεις έχουν το ίδιο απόθεμα για την ίδια τιμή προειδοποίησης και την ίδια ημερομηνία λήξης.
Αυτή η αρχή ισχύει για ευρωπαϊκές επιλογές και όχι για αμερικανικές επιλογές. Οι ευρωπαϊκές επιλογές μπορούν να ασκηθούν μόνο κατά την ημερομηνία λήξης, ενώ οι αμερικανικές επιλογές μπορούν να ασκηθούν οποιαδήποτε στιγμή πριν από την ημερομηνία λήξης.
Σύμφωνα με την αρχή του Put-Call Parity, η τιμή μιας κλήσης και η προεξοφλημένη παρούσα αξία της τιμής προειδοποίησης θα πρέπει να είναι ίση με την τιμή του put και την τρέχουσα τιμή αγοράς του αποθέματος. Η σχέση εξηγείται με την εξίσωση που αναφέρεται παρακάτω:
Ο τύπος για ισοτιμία put-call είναι:
C + PV (S) = P + MP
Στην παραπάνω εξίσωση, το C αντιπροσωπεύει την αξία της κλήσης. Το PV (S) είναι η παρούσα αξία της τιμής προειδοποίησης που προεξοφλείται χρησιμοποιώντας ένα ποσοστό χωρίς κίνδυνο. P είναι η τιμή του δικαιώματος πώλησης ενώ το MP είναι η τρέχουσα τιμή αγοράς του αποθέματος.
Εάν η εξίσωση δεν είναι καλή, υπάρχει ένα πεδίο διαιτησίας, δηλαδή κέρδος χωρίς κίνδυνο.
Παραδείγματα
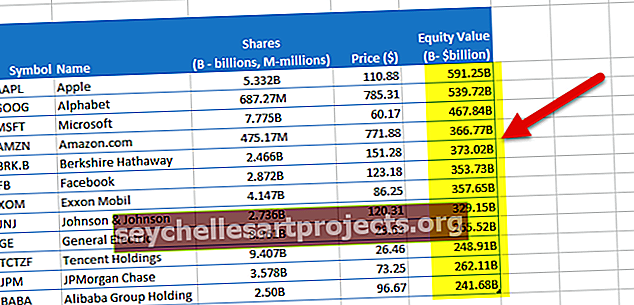
Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου Put Call Parity Formula Excel - Πρότυπο Put Call Parity Formula ExcelΠαράδειγμα # 1
Ας πάρουμε ένα παράδειγμα μετοχής της ABC Ltd. Το μερίδιο της ABC Ltd διαπραγματεύεται στα 93 $ την 1η Ιανουαρίου 2019. Η κλήση της τιμής προειδοποίησης των $ 100 για την 31η Δεκεμβρίου 2019 Η λήξη διαπραγματεύεται στα 8 $. Ενώ ο κίνδυνος- Το δωρεάν επιτόκιο στην αγορά είναι 8%.
Λύση:
Χρησιμοποιήστε τα παρακάτω δεδομένα για τον υπολογισμό της ισοτιμίας κλήσης.

Επομένως, για να καθιερωθεί η αρχή της ισοτιμίας κλήσης, η ακόλουθη εξίσωση πρέπει να ισχύει:

8 + PV των 100 με έκπτωση 8% = P + 93
δηλαδή 8 + 92,59 = P +93
Ρ = 92,59 + 8 - 93
Η εξίσωση Put Call Parity θα είναι -

Τιμή put put Option = 7.59
Εάν η πραγματική αγοραία τιμή του put δεν είναι ίση με 7,59 $, θα υπάρξει μια ευκαιρία arbitrage.
Αυτή η ευκαιρία arbitrage δεν υπάρχει για μια πραγματική αγορά για πολύ. Οι διαιτητές στην αγορά εκμεταλλεύονται αυτήν την ευκαιρία γρήγορα και οι τιμές των αποθεμάτων ή των επιλογών προσαρμόζονται αυτόματα για να καθορίσουν την ισοτιμία put-call.
Σε αυτό το παράδειγμα, εάν η πραγματική αγοραία τιμή του put είναι 9 $, οι διαιτητές θα αρχίσουν να πωλούν ή να μειώσουν το put που τελικά θα αυξήσει την προσφορά του put ανάλογα με τη ζήτησή του και κατά συνέπεια η τιμή του put θα μειωθεί στα 7,59 $.
Είχαμε υποθέσει την τιμή της μετοχής, την τιμή κλήσης και την τιμή χωρίς κίνδυνο στο παραπάνω παράδειγμα και υπολογίσαμε την τιμή μιας επιλογής put. Ωστόσο, μπορούμε επίσης να πάρουμε ένα άλλο παράδειγμα όπου μπορεί να θεωρηθεί η τιμή του put και μπορεί να υπολογιστεί οποιοδήποτε άλλο στοιχείο της εξίσωσης.
Παράδειγμα # 2
Σε αυτό το παράδειγμα, ας υποθέσουμε ότι η κλήση των μετοχών της XYZ Ltd. Η τιμή προειδοποίησης των 350 $ διαπραγματεύεται στα 29 $ την 1η Ιανουαρίου 2019. Η ημερομηνία λήξης της ίδιας είναι η 31η Δεκεμβρίου 2019. Διάθεση του αποθέματος για την ίδια προειδοποίηση τιμή και η ίδια ημερομηνία λήξης διαπραγματεύεται 15 $. Το επιτόκιο χωρίς κίνδυνο στην αγορά είναι 10%. Ας υπολογίσουμε ποια θα πρέπει να είναι η τρέχουσα αγοραία τιμή του αποθέματος της XYZ Ltd:
Λύση:
Χρησιμοποιήστε τα παρακάτω δεδομένα για τον υπολογισμό της ισοτιμίας κλήσης.

Ο υπολογισμός της τιμής αγοράς μπορεί να γίνει ως εξής:

C + PV (S) = P + MP
29 + PV (350) με ρυθμό 10% = 15 + MP
δηλαδή 29 + 318,18 = 15 + MP
MP = 318,18 + 29 - 15
Η τιμή αγοράς θα είναι -

Τιμή αγοράς = 332,18
Εάν η πραγματική αγοραία τιμή του αποθέματος δεν είναι ίση με 332,18, θα υπάρξει ευκαιρία arbitrage.
Παράδειγμα # 3
Σε συνέχεια των παραδοχών που λαμβάνονται στο παράδειγμα 2, Εάν η πραγματική αγοραία τιμή του αποθέματος είναι 350, αυτό σημαίνει είτε το απόθεμα διαπραγματεύεται σε υψηλότερη τιμή είτε η κλήση διαπραγματεύεται σε χαμηλότερη τιμή ή το εμπόριο διαπραγματεύεται σε υψηλότερη τιμή. Για να κερδίσει ένα κέρδος χωρίς κίνδυνο, ένας διαιτητής θα κάνει τα εξής:
Λύση:
Την 1η Ιανουαρίου 2019
Θα αγοράσει μια κλήση επενδύοντας 29 $ και θα επενδύσει 318,18 $ @ επιτόκιο χωρίς κίνδυνο 10% για ένα χρόνο. Θα πουλήσει put επιλογές είναι $ 15 και επίσης σύντομη πώληση το απόθεμα στα 350.
Ο υπολογισμός της καθαρής εισροής μετρητών μπορεί να γίνει ως εξής:

Η καθαρή εισροή μετρητών στην τσέπη του την 1η Ιανουαρίου 2019 θα είναι 350 + 15 - 318,18 - 29.
Καθαρή εισροή μετρητών = 17,82
Σενάριο # 1 - Ας υποθέσουμε ότι στις 31 Δεκεμβρίου 2019, το χρηματιστήριο διαπραγματεύεται στα 390 $
Η κλήση του θα πάρει 40 $. Από την επένδυση χωρίς κίνδυνο ύψους 318,18 $, θα λάβει 350 $. Δεν θα χρειαστεί να πληρώσει τίποτα στην επιλογή put. Ωστόσο, θα πρέπει να αγοράσει το μερίδιο από την τρέχουσα αγορά στα 390 $, τα οποία είχε αρχικά πωλήσει.
Ο υπολογισμός της καθαρής ταμειακής εκροής μπορεί να γίνει ως εξής:

Η καθαρή ταμειακή εκροή / εισροή στις 31 Δεκεμβρίου 2019 θα είναι 350 + 40 - 390.
Εισροή / Εκροή = 0
Σενάριο # 2 - Τώρα, ας υποθέσουμε ότι η τιμή μετοχής στις 31 Δεκεμβρίου 2019 είναι 250
Σε αυτήν την περίπτωση, το τηλεφώνημά του δεν θα φέρει τίποτα, ενώ θα πρέπει να πληρώσει $ 100 για το put. Η επένδυσή του χωρίς κίνδυνο θα του πάρει 350 $. Ταυτόχρονα, θα πρέπει να αγοράσει το μερίδιο από την τρέχουσα αγορά στα 250 $, τα οποία είχε αρχικά πωλήσει.
Ο υπολογισμός της καθαρής ταμειακής εκροής μπορεί να γίνει ως εξής:

Η καθαρή ταμειακή εκροή / εισροή στις 31 Δεκεμβρίου 2019 θα είναι 350 - 250 -100.
Εισροή / Εκροή = 0
Ανεξάρτητα από την τιμή ενός αποθέματος κατά την ημερομηνία λήξης, η ταμειακή ροή του κατά την εν λόγω ημερομηνία θα είναι 0, ενώ είχε ήδη κερδίσει 17. 82 $ την 1η Ιανουαρίου 2019. Αυτό οφείλεται στη διαθεσιμότητα ευκαιριών arbitrage στην αγορά. Πολύ σύντομα, οι διαιτητές που είναι παρόντες στην αγορά θα εκμεταλλευτούν αυτήν την ευκαιρία και οι τιμές του αποθέματος και των επιλογών θα προσαρμοστούν για να ικανοποιήσουν την εξίσωση της ισοτιμίας put-call.
συμπέρασμα
Σημειώστε ότι σε μια ώριμη αγορά, αυτοί οι τύποι ευκαιριών arbitrage σχεδόν δεν υπάρχουν. Περαιτέρω, το τέλος συναλλαγής και οι φόροι στην πραγματική αγορά ενδέχεται να δυσκολεύουν ή να είναι αδύνατο να επωφεληθούν από οποιαδήποτε ανακρίβεια, εάν υπάρχει. Για να αναλυθεί η ισοτιμία put-call, οι τιμές των επιλογών και η τρέχουσα τιμή αγοράς του αποθέματος μπορούν να ληφθούν από το χρηματιστήριο. Το επιτόκιο που παρέχεται από τα κρατικά ομόλογα μπορεί να ληφθεί ως επιτόκιο χωρίς κίνδυνο. Ωστόσο, όλες οι μεταβλητές και οι κανόνες της αγοράς πρέπει να λαμβάνονται υπόψη κατά την ανάλυση της ισοτιμίας «put-call» για οποιοδήποτε συγκεκριμένο απόθεμα.