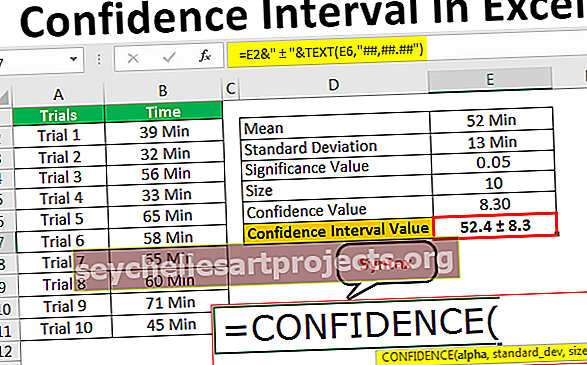
Διαφορά μεταξύ δοκιμής Z και δοκιμής δοκιμής υπόθεσης
Διαφορές μεταξύ Z-Test και T-Test
Η δοκιμή Z είναι η στατιστική υπόθεση που χρησιμοποιείται για να προσδιοριστεί ότι εάν τα δύο δείγματα μέσων που υπολογίστηκαν είναι διαφορετικά σε περίπτωση που η τυπική απόκλιση είναι διαθέσιμη και το δείγμα είναι μεγάλο ενώ το τεστ T χρησιμοποιείται για να προσδιοριστεί ο τρόπος μέσων όρων διαφορετικών συνόλων δεδομένων διαφέρει μεταξύ τους σε περίπτωση που η τυπική απόκλιση ή η διακύμανση δεν είναι γνωστή.
Οι δοκιμές Z και t-test είναι οι δύο στατιστικές μέθοδοι που περιλαμβάνουν ανάλυση δεδομένων που έχει εφαρμογές στην επιστήμη, στις επιχειρήσεις και σε πολλούς άλλους κλάδους. Το t-test μπορεί να αναφέρεται σε ένα τεστ univariate υπόθεσης που βασίζεται σε t-στατιστική, όπου ο μέσος όρος δηλαδή ο μέσος όρος είναι γνωστός και η διακύμανση του πληθυσμού δηλαδή η τυπική απόκλιση προσεγγίζεται από το δείγμα. Από την άλλη πλευρά, το Z-test, είναι επίσης ένα univariate τεστ που βασίζεται σε μια τυπική κανονική κατανομή.

Χρήσεις
# 1 - Δοκιμή Z
Ο τύπος Z-test, όπως αναφέρθηκε προηγουμένως, είναι οι στατιστικοί υπολογισμοί που μπορούν να χρησιμοποιηθούν για τη σύγκριση των μέσων όρων πληθυσμού με τους δείκτες. Το z-test θα σας πει πόσο μακριά, σε όρους τυπικών αποκλίσεων, ένα σημείο δεδομένων είναι από το μέσο όρο ενός συνόλου δεδομένων. Ένα z-test θα κάνει μια σύγκριση ενός δείγματος με έναν καθορισμένο πληθυσμό που χρησιμοποιείται συνήθως για την αντιμετώπιση προβλημάτων που σχετίζονται με μεγάλα δείγματα (δηλ. N> 30). Κυρίως, είναι πολύ χρήσιμα όταν είναι γνωστή η τυπική απόκλιση.
# 2 - Δοκιμή T
Οι δοκιμές T είναι επίσης υπολογισμοί που μπορούν να χρησιμοποιηθούν για τον έλεγχο μιας υπόθεσης, αλλά είναι πολύ χρήσιμοι όταν πρέπει να προσδιορίσουμε εάν υπάρχει στατιστικά σημαντική σύγκριση μεταξύ των 2 ανεξάρτητων ομάδων δειγμάτων. Με άλλα λόγια, ένα t-test ρωτά αν η σύγκριση μεταξύ των μέσων όρων 2 ομάδων είναι απίθανο να έχει συμβεί λόγω τυχαίας πιθανότητας. Συνήθως, οι δοκιμές t είναι πιο κατάλληλες όταν αντιμετωπίζετε προβλήματα με περιορισμένο μέγεθος δείγματος (δηλ. N <30).
Z-Test vs T-Test Infographics
Εδώ σας παρέχουμε τις 5 πρώτες διαφορές μεταξύ του z-test έναντι του t-test που πρέπει να γνωρίζετε.

Βασικές διαφορές
- Μία από τις πιο σημαντικές προϋποθέσεις για τη διεξαγωγή δοκιμής t είναι ότι η τυπική απόκλιση πληθυσμού ή η διακύμανση είναι άγνωστη. Αντίθετα, ο τύπος διακύμανσης πληθυσμού όπως αναφέρεται παραπάνω πρέπει να θεωρείται ότι είναι γνωστός ή γνωστός σε περίπτωση δοκιμής z.
- Το τεστ t όπως αναφέρεται παραπάνω βασίζεται στην κατανομή t του Student. Αντιθέτως, η δοκιμή z εξαρτάται από την υπόθεση ότι η κατανομή των μέσων δειγματοληψίας θα είναι φυσιολογική. Τόσο η κανονική κατανομή όσο και η κατανομή t του μαθητή φαίνεται η ίδια, καθώς και τα δύο είναι σε σχήμα καμπάνας και συμμετρικά. Ωστόσο, διαφέρουν σε μία από τις περιπτώσεις που κατά την κατανομή, υπάρχει λιγότερος χώρος στο κέντρο και περισσότερο στις ουρές τους.
- Το Z-test χρησιμοποιείται όπως δίνεται στον παραπάνω πίνακα όταν το μέγεθος του δείγματος είναι μεγάλο, το οποίο είναι n> 30, και το t-test είναι κατάλληλο όταν το μέγεθος του δείγματος δεν είναι μεγάλο που είναι μικρό, δηλαδή n <30.
Συγκριτικός πίνακας Z-Test vs T-Test
| Βάση | Δοκιμή Z | Τ-δοκιμή | ||
| Βασικός ορισμός | Το Z-test είναι ένα είδος δοκιμής υπόθεσης που εξακριβώνει εάν οι μέσοι όροι των 2 συνόλων δεδομένων είναι διαφορετικοί μεταξύ τους όταν δίνεται τυπική απόκλιση ή διακύμανση. | Το t-test μπορεί να αναφέρεται σε ένα είδος παραμετρικής δοκιμής που εφαρμόζεται σε μια ταυτότητα, πώς οι μέσες τιμές 2 συνόλων δεδομένων διαφέρουν μεταξύ τους όταν δεν παρέχεται η τυπική απόκλιση ή διακύμανση. | ||
| Ποικιλία πληθυσμού | Η διακύμανση πληθυσμού ή η τυπική απόκλιση είναι γνωστή εδώ. | Η διακύμανση πληθυσμού ή η τυπική απόκλιση είναι άγνωστη εδώ. | ||
| Το μέγεθος του δείγματος | Το μέγεθος του δείγματος είναι μεγάλο | Εδώ το μέγεθος δείγματος είναι μικρό. | ||
| Βασικές υποθέσεις |
|
|
||
| Με βάση (έναν τύπο διανομής) | Με βάση την Κανονική κατανομή. | Με βάση την κατανομή Student-t. |
συμπέρασμα
Σε και σε μεγαλύτερο βαθμό, και οι δύο αυτές δοκιμές είναι σχεδόν παρόμοιες, αλλά η σύγκριση έρχεται μόνο στις συνθήκες τους για την εφαρμογή τους, πράγμα που σημαίνει ότι η δοκιμή t είναι πιο κατάλληλη και εφαρμόσιμη όταν το μέγεθος του δείγματος δεν υπερβαίνει τις τριάντα μονάδες. Ωστόσο, εάν είναι μεγαλύτερη από τριάντα μονάδες, θα πρέπει να χρησιμοποιήσετε μια δοκιμή z. Ομοίως, υπάρχουν και άλλες προϋποθέσεις, οι οποίες θα καταστήσουν σαφές ότι ποια δοκιμή πρέπει να πραγματοποιηθεί σε μια κατάσταση.
Λοιπόν, υπάρχουν επίσης διαφορετικές δοκιμές όπως δοκιμή f, δίπλευρη έναντι μονής ουράς κ.λπ., οι στατιστικοί πρέπει να είναι προσεκτικοί κατά την εφαρμογή τους μετά την ανάλυση της κατάστασης και στη συνέχεια να αποφασίσουν ποια θα χρησιμοποιήσουν. Ακολουθεί ένα δείγμα γραφήματος για αυτό που συζητήσαμε παραπάνω.