seychellesartprojects.org

Ορισμός συντελεστή συσχέτισης Pearson

Ο συντελεστής συσχέτισης Pearson, επίσης γνωστός ως στατιστικός έλεγχος Pearson R, μετρά την ισχύ μεταξύ των διαφορετικών μεταβλητών και των σχέσεών τους. Κάθε φορά που πραγματοποιείται οποιαδήποτε στατιστική δοκιμή μεταξύ των δύο μεταβλητών, τότε είναι πάντα καλή ιδέα για το άτομο που κάνει ανάλυση να υπολογίσει την τιμή του συντελεστή συσχέτισης για να γνωρίζει πόσο ισχυρή είναι η σχέση μεταξύ των δύο μεταβλητών.

Ο συντελεστής συσχέτισης του Pearson επιστρέφει μια τιμή μεταξύ -1 και 1. Η ερμηνεία του συντελεστή συσχέτισης έχει ως εξής:

• Εάν ο συντελεστής συσχέτισης είναι -1, αυτό δείχνει μια ισχυρή αρνητική σχέση. Υπονοεί μια τέλεια αρνητική σχέση μεταξύ των μεταβλητών.
• Εάν ο συντελεστής συσχέτισης είναι 0, δεν δείχνει καμία σχέση.
• Εάν ο συντελεστής συσχέτισης είναι 1, δείχνει μια ισχυρή θετική σχέση. Υπονοεί μια τέλεια θετική σχέση μεταξύ των μεταβλητών.

Μια υψηλότερη απόλυτη τιμή του συντελεστή συσχέτισης δείχνει μια ισχυρότερη σχέση μεταξύ των μεταβλητών. Έτσι, ένας συντελεστής συσχέτισης 0,78 υποδηλώνει μια ισχυρότερη θετική συσχέτιση σε σύγκριση με μια τιμή, π.χ. Παρομοίως, ένας συντελεστής συσχέτισης -0,87 υποδηλώνει ισχυρότερη αρνητική συσχέτιση σε σύγκριση με τον συντελεστή συσχέτισης του λόγου -0,40

Με άλλα λόγια, εάν η τιμή είναι στο θετικό εύρος, τότε δείχνει ότι η σχέση μεταξύ των μεταβλητών συσχετίζεται θετικά και οι δύο τιμές μειώνονται ή αυξάνονται μαζί. Από την άλλη πλευρά, εάν η τιμή βρίσκεται στο αρνητικό εύρος, τότε δείχνει ότι η σχέση μεταξύ των μεταβλητών συσχετίζεται αρνητικά και ότι και οι δύο τιμές θα πάνε στην αντίθετη κατεύθυνση.

Τύπος συντελεστή συσχέτισης Pearson

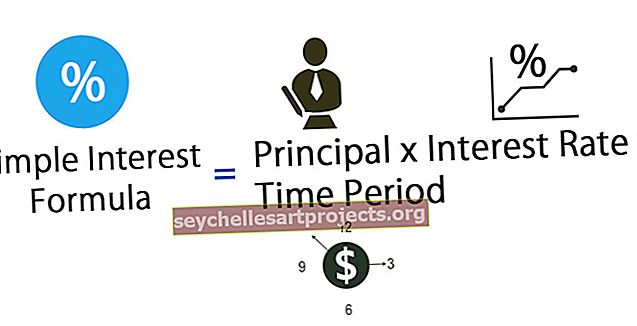
Ο τύπος συντελεστή συσχέτισης Pearson έχει ως εξής,

Που,

• r = Συντελεστής Pearson
• n = αριθμός των ζευγαριών του αποθέματος
• ∑xy = άθροισμα των προϊόντων των ζευγαρωμένων αποθεμάτων
• ∑x = άθροισμα των βαθμολογιών x
• ∑y = άθροισμα των αποτελεσμάτων y
• ∑x2 = άθροισμα των τετραγώνων x αποτελεσμάτων
• ∑y2 = άθροισμα των αποτελεσμάτων τετραγώνου y

Εξήγηση

Βήμα 1: Ανακαλύψτε τον αριθμό των ζευγών μεταβλητών, που συμβολίζεται με το n. Ας υποθέσουμε ότι το x αποτελείται από 3 μεταβλητές - 6, 8, 10. Ας υποθέσουμε ότι το y αποτελείται από αντίστοιχες 3 μεταβλητές 12, 10, 20.

Βήμα 2: Καταγράψτε τις μεταβλητές σε δύο στήλες.

Βήμα 3: Μάθετε το προϊόν των x και y στην 3η στήλη.

Βήμα 4: Μάθετε το άθροισμα των τιμών όλων των μεταβλητών x και όλων των μεταβλητών y. Γράψτε τα αποτελέσματα στο κάτω μέρος της 1ης και της 2ης στήλης. Γράψτε το άθροισμα x * y στην 3η στήλη.

Βήμα 5: Μάθετε x2 και y2 στην 4η και 5η στήλη και το άθροισμά τους στο κάτω μέρος των στηλών.

Βήμα 6: Εισαγάγετε τις τιμές που βρίσκονται παραπάνω στον τύπο και επιλύστε το.

r = 3 * 352-24 * 42 / √ (3 * 200-242) * (3 * 644-422)

= 0,7559

Παράδειγμα συντελεστή συσχέτισης Pearson R

Μπορείτε να κάνετε λήψη αυτού του προτύπου Excel Συντελεστής συσχέτισης Pearson εδώ - Πρότυπο Excel Συντελεστής συσχέτισης Pearson

Παράδειγμα 1

Σε αυτό το παράδειγμα με τη βοήθεια των παρακάτω λεπτομερειών στον πίνακα των 6 ατόμων που έχουν διαφορετική ηλικία και διαφορετικά βάρη που δίνονται παρακάτω για τον υπολογισμό της τιμής του Pearson R

Λύση:

Για τον υπολογισμό του συντελεστή συσχέτισης Pearson, θα υπολογίσουμε πρώτα τις ακόλουθες τιμές,

Εδώ ο συνολικός αριθμός ατόμων είναι 6 έτσι, n = 6

Τώρα ο υπολογισμός του Pearson R έχει ως εξής,

• r = (n (∑xy) - (∑x) (∑y)) / (√ [n ∑x2- (∑x) 2] [n ∑y2– (∑y) 2)
• r = (6 * (13937) - (202) (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• r = (6 * (13937) - (202) * (409)) / (√ [6 * 7280 - (202) 2] * [6 * 28365- (409) 2)
• r = (83622- 82618) / (√ [43680 -40804] * [170190- 167281]
• r = 1004 / (√ [2876] * [2909)
• r = 1004 / (√ 8366284)
• r = 1004 / 2892.452938
• r = 0,35

Έτσι, η τιμή του συντελεστή συσχέτισης Pearson είναι 0,35

Παράδειγμα # 2

Υπάρχουν 2 μετοχές - Α και Β. Οι τιμές των μετοχών τους σε συγκεκριμένες ημέρες έχουν ως εξής:

Μάθετε τον συντελεστή συσχέτισης Pearson από τα παραπάνω δεδομένα.

Λύση:

Πρώτον, θα υπολογίσουμε τις ακόλουθες τιμές.

Ο υπολογισμός του συντελεστή Pearson έχει ως εξής,

• r =  (5 * 1935-266 * 37) / ((5 * 14298- (266) ^ 2) * (5 * 283- (37) ^ 2)) ^ 0,5
• = -0.9088

Επομένως, ο συντελεστής συσχέτισης Pearson μεταξύ των δύο αποθεμάτων είναι -0.9088.

Πλεονεκτήματα

• Βοηθά να μάθουμε πόσο ισχυρή είναι η σχέση μεταξύ των δύο μεταβλητών. Όχι μόνο η παρουσία ή η απουσία συσχέτισης μεταξύ των δύο μεταβλητών υποδεικνύεται με τη χρήση του συντελεστή συσχέτισης Pearson, αλλά καθορίζει επίσης τον ακριβή βαθμό στον οποίο αυτές οι μεταβλητές συσχετίζονται.
• Χρησιμοποιώντας αυτήν τη μέθοδο, μπορεί κανείς να εξακριβώσει την κατεύθυνση της συσχέτισης, δηλαδή εάν η συσχέτιση μεταξύ δύο μεταβλητών είναι αρνητική ή θετική.

Μειονεκτήματα

• Ο συντελεστής συσχέτισης Pearson R δεν επαρκεί για να πει τη διαφορά μεταξύ των εξαρτώμενων μεταβλητών και των ανεξάρτητων μεταβλητών καθώς ο συντελεστής συσχέτισης μεταξύ των μεταβλητών είναι συμμετρικός. Για παράδειγμα, εάν ένα άτομο προσπαθεί να γνωρίζει τη σχέση μεταξύ του υψηλού στρες και της αρτηριακής πίεσης, τότε κάποιος μπορεί να βρει την υψηλή τιμή του συσχετισμού που δείχνει ότι το υψηλό στρες προκαλεί την αρτηριακή πίεση. Τώρα, εάν η μεταβλητή αλλάξει, τότε το αποτέλεσμα, στην περίπτωση αυτή, θα είναι επίσης το ίδιο που δείχνει ότι το άγχος προκαλείται από την αρτηριακή πίεση που δεν έχει νόημα. Έτσι, ο ερευνητής θα πρέπει να γνωρίζει τα δεδομένα που χρησιμοποιεί για τη διεξαγωγή της ανάλυσης.
• Χρησιμοποιώντας αυτήν τη μέθοδο δεν μπορεί κανείς να πάρει τις πληροφορίες σχετικά με την κλίση της γραμμής, καθώς δηλώνει μόνο εάν υπάρχει σχέση μεταξύ των δύο μεταβλητών ή όχι.
• Είναι πιθανό ότι ο συντελεστής συσχέτισης Pearson μπορεί να παρερμηνευθεί ειδικά σε περίπτωση ομοιογενών δεδομένων.
• Σε σύγκριση με τις άλλες μεθόδους υπολογισμού, αυτή η μέθοδος απαιτεί πολύ χρόνο για να φτάσει στα αποτελέσματα.

Σημαντικά σημεία

• Οι τιμές μπορούν να κυμαίνονται από την τιμή +1 έως την τιμή -1, όπου το +1 υποδεικνύει την τέλεια θετική σχέση μεταξύ των μεταβλητών που εξετάστηκαν, το -1 υποδεικνύει την τέλεια αρνητική σχέση μεταξύ των μεταβλητών που εξετάστηκαν και μια τιμή 0 δείχνει ότι δεν υπάρχει σχέση υπάρχει μεταξύ των υπό εξέταση μεταβλητών.
• Είναι ανεξάρτητη από τη μονάδα μέτρησης των μεταβλητών. Για παράδειγμα, εάν η μονάδα μέτρησης μιας μεταβλητής είναι σε χρόνια, ενώ η μονάδα μέτρησης της δεύτερης μεταβλητής είναι σε χιλιόγραμμα, ακόμη και τότε, η τιμή αυτού του συντελεστή δεν αλλάζει.
• Ο συντελεστής συσχέτισης μεταξύ των μεταβλητών είναι συμμετρικός που σημαίνει ότι η τιμή του συντελεστή συσχέτισης μεταξύ Υ και Χ ή Χ και Υ, θα παραμείνει η ίδια.

συμπέρασμα

Ο συντελεστής συσχέτισης Pearson είναι ο τύπος του συντελεστή συσχέτισης που αντιπροσωπεύει τη σχέση μεταξύ των δύο μεταβλητών που μετρώνται στο ίδιο διάστημα ή την ίδια κλίμακα αναλογίας. Μετρά την ισχύ της σχέσης μεταξύ των δύο συνεχών μεταβλητών.

Δεν δηλώνει μόνο την παρουσία ή την απουσία συσχέτισης μεταξύ των δύο μεταβλητών, αλλά καθορίζει επίσης την ακριβή έκταση στην οποία αυτές οι μεταβλητές συσχετίζονται. Είναι ανεξάρτητη από τη μονάδα μέτρησης των μεταβλητών όπου οι τιμές του συντελεστή συσχέτισης μπορούν να κυμαίνονται από την τιμή +1 έως την τιμή -1. Ωστόσο, δεν αρκεί να πούμε τη διαφορά μεταξύ των εξαρτημένων μεταβλητών και των ανεξάρτητων μεταβλητών.