seychellesartprojects.org

Ορισμός τιμής ωριμότητας

Η αξία λήξης είναι το ποσό που πρέπει να εισπραχθεί κατά την ημερομηνία λήξης ή κατά τη λήξη του μέσου / ασφάλειας που διατηρεί ο επενδυτής κατά τη χρονική του περίοδο και υπολογίζεται πολλαπλασιάζοντας το κύριο ποσό στο επιτοκιακό επιτόκιο που υπολογίζεται περαιτέρω με ένα επιτόκιο συν ενδιαφέροντος για τη δύναμη που είναι χρονική περίοδος.

Τύπος τιμής ωριμότητας

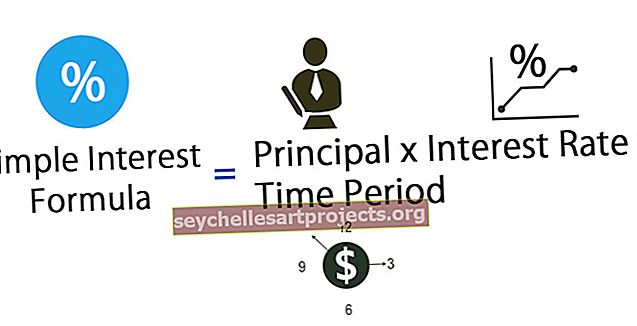
Ο τύπος για τον υπολογισμό της τιμής λήξης είναι ως εξής:

MV = P * (1 + r) n

Που,

• Το MV είναι η τιμή ωριμότητας
• P είναι το κύριο ποσό
• r είναι το επιτόκιο που ισχύει
• n είναι ο αριθμός των διαστημάτων σύνθεσης από την ώρα της ημερομηνίας κατάθεσης έως τη λήξη

Εξήγηση

Ο τύπος που χρησιμοποιείται για τον υπολογισμό της αξίας λήξης περιλαμβάνει τη χρήση του αρχικού ποσού που είναι το ποσό που επενδύεται στην αρχική περίοδο και το n είναι ο αριθμός των περιόδων για τις οποίες ο επενδυτής επενδύει και το r είναι το επιτόκιο που κερδίζεται σε αυτήν την επένδυση.

Όταν κάποιος παίρνει τη συχνότητα της σύνθεσης ως δύναμη για να το βαθμολογήσει παίρνει πολλαπλάσια που δεν είναι τίποτα άλλο από την ένωση και στη συνέχεια όταν το αποτέλεσμα πολλαπλασιάζεται με το κύριο ποσό, κάποιος παίρνει την τιμή ωριμότητας που μπορεί να έχει κάποιος.

Παραδείγματα τύπων τιμής ωριμότητας (με πρότυπο Excel)

Ας δούμε μερικά απλά έως προχωρημένα παραδείγματα του Maturity Value Formula για να το κατανοήσουμε καλύτερα.

Μπορείτε να πραγματοποιήσετε λήψη αυτού του προτύπου Formula Excel Maturity Value - Πρότυπο Formula Excel Value Maturity

Παράδειγμα # 1

Ο κ. Α επένδυσε 100.000 σε τραπεζική προκαταβολή στην ABC bank ltd. ABC bank ltd. πληρώνει 8,75% σε ετήσια βάση. Υπολογίστε το ποσό λήξης που θα πάρει ο κ. Α, εφόσον επενδύσει για 3 χρόνια.

Λύση:

Ο κ. Α έχει επενδύσει σε πάγια κατάθεση για 3 χρόνια και δεδομένου ότι συντίθεται κάθε χρόνο, το n θα είναι 3, το P είναι 100.000 και το r είναι 8,75%.

Έτσι, ο υπολογισμός της αξίας ωριμότητας έχει ως εξής,

• MV = 100.000 * (1 + 8,75%) 3
• MV = 100.000 * (1.286138672)

Η αξία ωρίμανσης θα είναι -

• MV = 128.613.87

Παράδειγμα # 2

Ο Τζον Μπράντσαου έχει υψηλό καθαρό περιουσιακό στοιχείο και έχει επενδύσει το 60% των επενδύσεών του σε μετοχές και τώρα πιστεύει ότι η αγορά θα πέσει στο μέλλον και ως εκ τούτου θέλει να επενδύσει προσωρινά κεφάλαια σε χρέος για να αποφύγει τον κίνδυνο και ως εκ τούτου σκέφτεται επένδυση σε CD που είναι συντομογραφία του Πιστοποιητικού Κατάθεσης.

Η Vista Limited έχει εκδώσει CD, το οποίο δηλώνει ότι θα πληρώσει τόκους 9% που θα προστίθενται κάθε μήνα Ας υποθέσουμε τώρα ότι ο κ. Τζον έχει επενδύσει το 30% των επενδύσεών του, δηλαδή 150.000 $ για 2 χρόνια. Υπολογίστε το ποσό λήξης που θα λάβει ο κ. John στο τέλος των 2 ετών.

Λύση:

Ο κ. John έχει επενδύσει στο Πιστοποιητικό Κατάθεσης για 2 χρόνια και δεδομένου ότι συντίθεται μηνιαίως, το n θα είναι 2 x 12, το οποίο είναι 24, το P είναι 150.000 $ και το r είναι 9,00% το οποίο ετησίως και επομένως το μηνιαίο επιτόκιο θα είναι 9/12, δηλαδή 0,75%.

Έτσι, ο υπολογισμός της αξίας ωριμότητας έχει ως εξής,

• MV = 150.000 $ * (1 + 0,75%) 24
• = 150.000 $ * (1.196413529)

Η αξία ωρίμανσης θα είναι -

• MV = 179.462,03 $

Ως εκ τούτου, ο κ. John θα λάβει 179.462,03 $ στο τέλος των 2 ετών.

Τύπος τιμής ωριμότητας - Παράδειγμα # 3

Η Κάρολ είναι 45 ετών γυναίκα που εργάζεται ως διευθυντής σε ένα MNC που βρίσκεται στη Νέα Υόρκη. Σκέφτεται ένα πρόγραμμα συνταξιοδότησης που του προτάθηκε από έναν σύμβουλο επενδύσεων που τον συμβουλεύει να επενδύσει ένα εφάπαξ ποσό 1.000.000 $ στο εγγυημένο πρόγραμμα συνταξιοδότησής του έως ότου συνταξιοδοτηθεί σε ηλικία 60 ετών. 3.744.787,29 $ και αυτό το σχέδιο της φαίνεται επικερδές. Ωστόσο, ο σύμβουλος επενδύσεων της είπε ότι συντίθεται ανά τρίμηνο και το ποσοστό απόδοσης που θα κερδίσει θα είναι 12%.

Ωστόσο, δεν είναι πεπεισμένη με το ποσοστό απόδοσης που λέει ότι θα κερδίσει. Πρέπει να υπολογίσετε το ποσοστό απόδοσης που θα κερδίσει σε αυτήν την επένδυση χρησιμοποιώντας τον τύπο τιμής λήξης και να ενημερώσετε εάν ο σύμβουλος επενδύσεων έχει κάνει μια σωστή δήλωση ή έχει μπλόφα για την απόδοση;

Λύση:

Η Carol θα επενδύσει στο εγγυημένο πρόγραμμα συνταξιοδότησης για 15 χρόνια, ο χρόνος που απομένει μέχρι να συνταξιοδοτηθεί σε ηλικία 60 ετών και δεδομένου ότι είναι ανά τρίμηνο, το n θα είναι 15 * 4 που είναι 60, το P είναι 1.000.000 $ και r πρέπει να μάθουμε και Εδώ μας δίνεται η τιμή λήξης ως 3.744.787,29 $

Μπορούμε να χρησιμοποιήσουμε τον παρακάτω τύπο τιμής λήξης και να προσθέσουμε τα στοιχεία και να φτάσουμε στο επιτόκιο.

MV = P * (1 + r) n

• 3.744.787.29 = 1.000.000 x (1 + r) (60)
• 3.74478729 = (1 + r) 60
• r = (3.7447829 - 1) 1/60

Έτσι, το Τριμηνιαίο Επιτόκιο θα είναι -

• r = 2,23% τριμηνιαία

Το ετήσιο επιτόκιο θα είναι -

• r (ετήσια) = 2,23 x 4
• = 8,90% ετησίως

Ως εκ τούτου, η δήλωση ενός επενδυτικού συμβούλου ότι θα κερδίσει 12% είναι λανθασμένη.

Υπολογιστής τιμής ωριμότητας

Μπορείτε να χρησιμοποιήσετε τον ακόλουθο Υπολογιστή Τιμής Ωριμότητας.

Π
ρ
ν
MV

MV = P * (1 + r) n

0 * (1 + 0) 0 = 0

Συνάφεια και χρήσεις

Είναι σημαντικό για αυτούς να είναι σε θέση να υπολογίσουν την αξία λήξης ενός χαρτονομίσματος, ώστε να μπορούν να γνωρίζουν πόσο θα πρέπει να πληρώσει μια επιχείρηση ή η εταιρεία ή η επιχείρηση όταν θα λήξει. Οι σύμβουλοι επενδύσεων χρησιμοποιούν αυτήν τη φόρμουλα για να συμβουλεύουν τους πελάτες επί τόπου του προγράμματος που πωλούν και όπως πόσα χρήματα θα έχουν στο χέρι.

Ένας μισθωτός χρήστης χρησιμοποιεί για να υπολογίσει την πάγια κατάθεση που πραγματοποιεί στις τράπεζες στις οποίες έχουν τους μισθωτούς λογαριασμούς τους. Ο τύπος μπορεί να χρησιμοποιηθεί για τον υπολογισμό του αντίστροφου επιτοκίου όταν κάποιος έχει αξία λήξης για να γνωρίζει το πραγματικό επιτόκιο που κερδίζεται από την επένδυση, όπως κάναμε στο τελευταίο μας παράδειγμα.