seychellesartprojects.org

Τι είναι το R Squared (R2) στο Regression;

Το R-squared (R2) είναι ένα σημαντικό στατιστικό μέτρο που είναι ένα μοντέλο παλινδρόμησης που αντιπροσωπεύει το ποσοστό της διαφοράς ή της διακύμανσης σε στατιστικούς όρους για μια εξαρτημένη μεταβλητή που μπορεί να εξηγηθεί από μια ανεξάρτητη μεταβλητή ή μεταβλητές. Εν ολίγοις, καθορίζει πόσο καλά τα δεδομένα θα ταιριάζουν με το μοντέλο παλινδρόμησης.

R τετραγωνικός τύπος

Για τον υπολογισμό του τετραγώνου R πρέπει να καθορίσετε τον συντελεστή συσχέτισης και έπειτα πρέπει να τετραγωνίσετε το αποτέλεσμα.

R τετραγωνικός τύπος = r2

Όπου r μπορεί να υπολογιστεί ο συντελεστής συσχέτισης ανά παρακάτω:

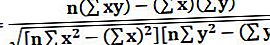
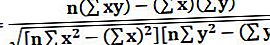
Που,

• r = Ο συντελεστής συσχέτισης
• n = αριθμός στο δεδομένο σύνολο δεδομένων
• x = πρώτη μεταβλητή στο περιβάλλον
• y = δεύτερη μεταβλητή

Εξήγηση

Εάν υπάρχει οποιαδήποτε σχέση ή συσχέτιση που μπορεί να είναι γραμμική ή μη γραμμική μεταξύ αυτών των δύο μεταβλητών, τότε υποδεικνύει εάν υπάρχει αλλαγή στην ανεξάρτητη μεταβλητή στην τιμή, τότε η άλλη εξαρτημένη μεταβλητή πιθανότατα θα αλλάξει στην αξία, π.χ. γραμμικά ή μη- γραμμικά.

Το αριθμητικό μέρος του τύπου διεξάγει μια δοκιμή αν κινούνται μαζί και αφαιρεί τις μεμονωμένες κινήσεις τους και τη σχετική αντοχή και των δύο κινούνται μαζί και το μέρος του παρονομαστή του τύπου κλιμακώνει τον αριθμητή λαμβάνοντας την τετραγωνική ρίζα του προϊόντος των διαφορών του μεταβλητές από τις τετραγωνικές μεταβλητές τους. Και όταν το τετράγωνο αυτό το αποτέλεσμα παίρνουμε το R τετράγωνο που δεν είναι παρά ο συντελεστής προσδιορισμού.

Παραδείγματα

Μπορείτε να κατεβάσετε αυτό το πρότυπο R Squared Formula Excel εδώ - Πρότυπο R Squared Formula Excel

Παράδειγμα # 1

Εξετάστε τις ακόλουθες δύο μεταβλητές x και y, πρέπει να υπολογίσετε το R Squared in Regression.

Λύση:

Χρησιμοποιώντας τον παραπάνω τύπο, πρέπει πρώτα να υπολογίσουμε τον συντελεστή συσχέτισης.

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 4.

Ας εισάγουμε τώρα τις τιμές στον τύπο για να φτάσουμε στο σχήμα.

r = (4 * 26,046,25) - (265,18 * 326,89) / √ [(4 * 21,274,94) - (326,89) 2] * [(4 * 31,901,89) - (326,89) 2]

r = 17,501,06 / 17,512,88

Συντελεστής συσχέτισης θα είναι-

r = 0,99932480

Έτσι, ο υπολογισμός θα έχει ως εξής,

r2 = (0,99932480) 2

R τετραγωνικός τύπος στην παλινδρόμηση

r2 = 0,998650052

Παράδειγμα # 2

Η Ινδία μια αναπτυσσόμενη χώρα θέλει να πραγματοποιήσει μια ανεξάρτητη ανάλυση εάν οι αλλαγές στις τιμές του αργού πετρελαίου έχουν επηρεάσει την αξία της ρουπίας της. Ακολουθεί η ιστορία της τιμής του αργού πετρελαίου Brent και της αποτίμησης ρουπίων και έναντι των δολαρίων που επικρατούσαν κατά μέσο όρο για τα έτη ανά παρακάτω.

Η RBI, η κεντρική τράπεζα της Ινδίας, σας πλησίασε για να παρουσιάσετε το ίδιο στην επόμενη συνάντηση. Προσδιορίστε εάν οι κινήσεις στο αργό πετρέλαιο επηρεάζουν τις κινήσεις σε ρουπία ανά δολάριο;

Λύση:

Χρησιμοποιώντας τον τύπο για την παραπάνω συσχέτιση, μπορούμε πρώτα να υπολογίσουμε τον συντελεστή συσχέτισης. Αντιμετώπιση της μέσης τιμής του αργού πετρελαίου ως μία μεταβλητή, π.χ. x και αντιμετώπιση της ρουπίας ανά δολάριο ως άλλη μεταβλητή ως y.

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 6.

Ας εισάγουμε τώρα τις τιμές στον τύπο για να φτάσουμε στο σχήμα.

r = (6 * 23592.83) - (356.70 * 398.59) / √ [(6 * 22829.36) - (356.70) 2] * [(6 * 26529.38) - (398.59) 2]

r = -620,06 / 1,715,95

Συντελεστής συσχέτισης θα είναι-

r = -0.3614

Έτσι, ο υπολογισμός θα έχει ως εξής,

r2 = (-0.3614) 2

R τετραγωνικός τύπος στην παλινδρόμηση

r2 = 0.1306

Ανάλυση: Φαίνεται ότι υπάρχει μια μικρή σχέση μεταξύ των αλλαγών στις τιμές του αργού πετρελαίου και των αλλαγών στην τιμή της ινδικής ρουπίας. Καθώς η τιμή του αργού πετρελαίου αυξάνεται, οι αλλαγές στην ινδική ρουπία επηρεάζουν επίσης. Αλλά επειδή το R τετράγωνο είναι μόνο 13%, τότε οι αλλαγές στην τιμή του αργού πετρελαίου εξηγούν πολύ λιγότερο για τις αλλαγές στην ινδική ρουπία και η ινδική ρουπία υπόκειται σε αλλαγές και σε άλλες μεταβλητές, οι οποίες πρέπει να ληφθούν υπόψη.

Παράδειγμα # 3

Το εργαστήριο XYZ διεξάγει έρευνα σχετικά με το ύψος και το βάρος και ενδιαφέρεται να μάθει αν υπάρχει σχέση μεταξύ αυτών των μεταβλητών. Αφού συγκέντρωσε ένα δείγμα 5000 ατόμων για κάθε κατηγορία και κατέληξε με ένα μέσο βάρος και μέσο ύψος στη συγκεκριμένη ομάδα.

Ακολουθούν οι λεπτομέρειες που έχουν συγκεντρώσει.

Πρέπει να υπολογίσετε το R τετράγωνο και να συμπεράνετε εάν αυτό το μοντέλο εξηγεί τις διακυμάνσεις στο ύψος επηρεάζει τις διακυμάνσεις στο βάρος.

Λύση:

Χρησιμοποιώντας τον τύπο για την παραπάνω συσχέτιση, μπορούμε πρώτα να υπολογίσουμε τον συντελεστή συσχέτισης. Αντιμετωπίζοντας το ύψος ως μία μεταβλητή, πούμε x και αντιμετωπίζοντας το βάρος ως άλλη μεταβλητή ως y

Έχουμε όλες τις τιμές στον παραπάνω πίνακα με n = 6.

Ας εισάγουμε τώρα τις τιμές στον τύπο για να φτάσουμε στο σχήμα.

r = (7 * 74,058,67) - (1031 * 496,44) / √ [(7 * 153595 - (1031) 2] * [(7 * 35793,59) - (496,44) 2]

r = 6,581,05 / 7,075,77

Συντελεστής συσχέτισης θα είναι-

Συντελεστής συσχέτισης (r) = 0,930

Έτσι, ο υπολογισμός θα έχει ως εξής,

r2 = 0,865

Ανάλυση: Ο συσχετισμός είναι θετικός και φαίνεται ότι υπάρχει κάποια σχέση μεταξύ ύψους και βάρους καθώς το ύψος αυξάνει το βάρος του ατόμου φαίνεται επίσης να αυξάνεται. Ενώ το R2 προτείνει ότι το 86% των αλλαγών στο ύψος αποδίδει τις αλλαγές στο βάρος και το 14% είναι ανεξήγητες.

Συνάφεια και χρήσεις

Η συνάφεια του R τετραγώνου στο Regression είναι η ικανότητά του να βρει την πιθανότητα μελλοντικών γεγονότων να συμβούν στα δεδομένα προβλεπόμενα αποτελέσματα ή τα αποτελέσματα. Εάν προστεθούν περισσότερα δείγματα στο μοντέλο, τότε ο συντελεστής θα έδειχνε την πιθανότητα ή την πιθανότητα ενός νέου σημείου ή του νέου συνόλου δεδομένων να πέσει στη γραμμή. Ακόμη και αν και οι δύο μεταβλητές έχουν ισχυρή σύνδεση, ο προσδιορισμός δεν αποδεικνύει την αιτιότητα.

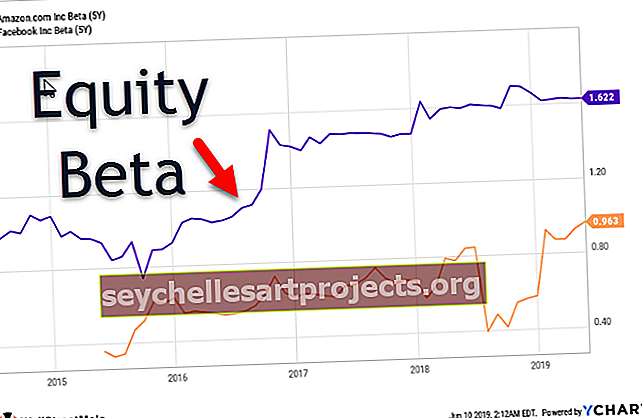
Μερικοί από τους χώρους στους οποίους χρησιμοποιείται κυρίως το R τετράγωνο είναι για την παρακολούθηση της απόδοσης των αμοιβαίων κεφαλαίων, για την παρακολούθηση του κινδύνου στα hedge funds, για να προσδιοριστεί πόσο καλά κινείται το απόθεμα με την αγορά, όπου το R2 θα προτείνει πόσες από τις κινήσεις στο απόθεμα μπορούν να εξηγηθούν από τις κινήσεις της αγοράς.