seychellesartprojects.org

Τύπος για τον υπολογισμό της τυπικής απόκλισης δείγματος

Η τυπική απόκλιση δείγματος αναφέρεται στη στατιστική μέτρηση που χρησιμοποιείται για τη μέτρηση του βαθμού με τον οποίο μια τυχαία μεταβλητή αποκλίνει από τη μέση τιμή του δείγματος και υπολογίζεται προσθέτοντας τα τετράγωνα της απόκλισης κάθε μεταβλητής από το μέσο όρο και στη συνέχεια διαιρέστε το αποτέλεσμα με μια σειρά μεταβλητών μείον και στη συνέχεια τον υπολογισμό της τετραγωνικής ρίζας στο excel του αποτελέσματος

Μαθηματικά, αντιπροσωπεύεται ως,

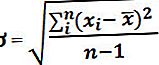
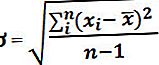
που

• x _i = με τυχαία μεταβλητή
• X = Μέσος όρος του δείγματος
• n = αριθμός μεταβλητών στο δείγμα

Υπολογισμός τυπικής απόκλισης δείγματος (βήμα προς βήμα)

• Βήμα 1: Πρώτον, συλλέξτε τυχαίες μεταβλητές από έναν πληθυσμό μεγάλου αριθμού μεταβλητών. Αυτές οι μεταβλητές θα αποτελέσουν δείγμα. Οι μεταβλητές υποδηλώνονται με x _i .
• Βήμα 2: Στη συνέχεια, προσδιορίστε τον αριθμό των μεταβλητών στο δείγμα και συμβολίζεται με το n.
• Βήμα 3: Στη συνέχεια, προσδιορίστε τη μέση τιμή του δείγματος προσθέτοντας όλες τις τυχαίες μεταβλητές και διαιρώντας το αποτέλεσμα με τον αριθμό των μεταβλητών στο δείγμα. Ο μέσος όρος δείγματος συμβολίζεται με x.

• Βήμα 4: Στη συνέχεια, υπολογίστε τη διαφορά μεταξύ κάθε μεταβλητής του δείγματος και του μέσου δείγματος, δηλαδή x _i - x.
• Βήμα 5: Στη συνέχεια, υπολογίστε το τετράγωνο όλων των αποκλίσεων, δηλαδή (x _i - x) 2.
• Βήμα 6: Στη συνέχεια, προσθέστε όλες τις τετραγωνικές αποκλίσεις, δηλαδή ∑ (x _i - x) 2.
• Βήμα 7: Στη συνέχεια, διαιρέστε το άθροισμα όλων των τετραγώνων αποκλίσεων με τον αριθμό των μεταβλητών στο δείγμα μείον μία δηλαδή (n - 1).
• Βήμα 8: Τέλος, ο τύπος τυπικής απόκλισης δείγματος υπολογίζεται υπολογίζοντας την τετραγωνική ρίζα του παραπάνω αναφερόμενου αποτελέσματος όπως φαίνεται παρακάτω.

Παραδείγματα

Μπορείτε να κατεβάσετε αυτό το πρότυπο δείγματος τυπικής απόκλισης τύπου Excel εδώ - Πρότυπο δείγματος τυπικής απόκλισης Excel

Παράδειγμα # 1

Ας πάρουμε το παράδειγμα ενός δείγματος 5 μαθητών που ρωτήθηκαν για να δουν πόσα μολύβια χρησιμοποιούσαν κάθε εβδομάδα. Υπολογίστε την τυπική απόκλιση δείγματος με βάση τις δικές τους απαντήσεις: 3, 2, 5, 6, 4

Δεδομένος,

• Μέγεθος δείγματος (n) = 5

Παρακάτω δίνονται δεδομένα για τον υπολογισμό της τυπικής απόκλισης δείγματος.

Μέσο δείγμα

Υπολογισμός του μέσου δείγματος

Μέσος δείκτης = (3 + 2 + 5 + 6 + 4) / 5

Μέσο δείγμα = 4

Τα τετράγωνα των αποκλίσεων κάθε μεταβλητής μπορούν να υπολογιστούν όπως παρακάτω,

• (3 - 4) 2 = 1
• (2 - 4) 2 = 4
• (5 - 4) 2 = 1
• (6 - 4) 2 = 4
• (4 - 4) 2 = 0

Τώρα, η τυπική απόκλιση δείγματος μπορεί να υπολογιστεί χρησιμοποιώντας τον παραπάνω τύπο ως,

• ơ = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}

Η απόκλιση θα είναι -

• ơ = 1,58

Επομένως, η τυπική απόκλιση δείγματος είναι 1,58.

Παράδειγμα # 2

Ας πάρουμε το παράδειγμα ενός γραφείου στη Νέα Υόρκη όπου περίπου 5.000 άτομα εργάζονται και πραγματοποιήθηκε έρευνα σε δείγμα 10 ατόμων για να προσδιοριστεί η μέση ηλικία του εργαζόμενου πληθυσμού. Προσδιορίστε την τυπική απόκλιση δείγματος με βάση τις ηλικίες των 10 ατόμων που δόθηκαν: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25

Δεδομένος,

• Μέγεθος δείγματος (n) = 10

Χρησιμοποιώντας τα παραπάνω δεδομένα θα υπολογίσουμε πρώτα τον μέσο όρο δείγματος

Μέσο δείγμα

Υπολογισμός του μέσου δείγματος

= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

Μέσο δείγμα = 27,8

Τα τετράγωνα των αποκλίσεων κάθε μεταβλητής μπορούν να υπολογιστούν όπως παρακάτω,

• (23 - 27,8) 2 = 23,04
• (27 - 27,8) 2 = 0,64
• (33 - 27,8) 2 = 27,04
• (28 - 27,8) 2 = 0,04
• (21 - 27,8) 2 = 46,24
• (24 - 27,8) 2 = 14,44
• (36 - 27,8) 2 = 67,24
• (32 - 27,8) 2 = 17,64
• (29 - 27,8) 2 = 1,44
• (25 - 27,8) 2 = 7,84

Απόκλιση

Τώρα, η απόκλιση μπορεί να υπολογιστεί χρησιμοποιώντας τον παραπάνω τύπο ως,

• ơ = √ {(23,04 + 0,64 + 27,04 + 0,04 + 46,24 +14,44 +67,24 + 17,64 + 1,44 + 7,84) / (10 - 1)}

Η απόκλιση θα είναι -

• ơ = 4,78

Μπορείτε να ανατρέξετε στο παραπάνω φύλλο excel για να κατανοήσετε τον λεπτομερή υπολογισμό.

Συνάφεια και χρήσεις

Η έννοια της τυπικής απόκλισης δείγματος είναι πολύ σημαντική από την οπτική γωνία ενός στατιστικολόγου επειδή συνήθως ένα δείγμα δεδομένων λαμβάνεται από μια ομάδα μεγάλων μεταβλητών (πληθυσμός) από την οποία ο στατιστικολόγος αναμένεται να εκτιμήσει ή να γενικεύσει τα αποτελέσματα για ολόκληρο τον πληθυσμό. Το μέτρο της τυπικής απόκλισης δεν αποτελεί εξαίρεση σε αυτό και ως εκ τούτου, ο στατιστικολόγος πρέπει να προβεί σε εκτίμηση της τυπικής απόκλισης του πληθυσμού με βάση το δείγμα που αντλήθηκε, και εκεί είναι που η παρέκκλιση αυτή αρχίζει να παίζει.